题目内容
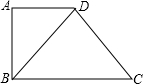
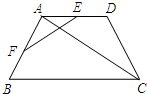
如图,在等腰梯形ABCD中,AD∥BC,M、N分别为AD、BC的中点,E、F分别是BM、CM 的中点.
的中点.
(1)求证:△ABM≌△CDM;
(2)四边形MENF是什么图形?请证明你的结论;
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?并请说明理由.
 的中点.
的中点.(1)求证:△ABM≌△CDM;
(2)四边形MENF是什么图形?请证明你的结论;
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?并请说明理由.
证明:(1)∵ABCD为等腰梯形,
∴AB=DC,∠A=∠D.
∵M是AD中点,
∴AM=DM.
∴△ABM≌△DCM.
(2)四边形MENF是菱形(若考生回答是平行四边形且给出证明,则此问题只能得2分)
由△ABM≌△DCM,得MB=MC,
∵E、F、N是MB、MC、BC的中点,
∴ME=
BM,MF=
MC,NF=
BM,NE=
MC.
∴ME=MF=FN=NE.
∴四边形MENF是菱形.
(3)梯形的高等于底边BC的一半连接MN,
∵MENF是正方形,
∴∠BMC=90°.
∵MB=MC,N是中点,
∴MN⊥BC且MN=
BC.
∴AB=DC,∠A=∠D.
∵M是AD中点,
∴AM=DM.
∴△ABM≌△DCM.
(2)四边形MENF是菱形(若考生回答是平行四边形且给出证明,则此问题只能得2分)
由△ABM≌△DCM,得MB=MC,
∵E、F、N是MB、MC、BC的中点,
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=MF=FN=NE.
∴四边形MENF是菱形.
(3)梯形的高等于底边BC的一半连接MN,
∵MENF是正方形,
∴∠BMC=90°.
∵MB=MC,N是中点,
∴MN⊥BC且MN=
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 (1)用t的代数式分别表示P、Q运动的路程;
(1)用t的代数式分别表示P、Q运动的路程;
