题目内容
在数学活动课上,小明做了一个梯形纸板,测得一底边长为7cm,高为12cm,两腰长分别为15cm和20cm,则该梯形纸板的另一底边长为______cm.
分为两种情况:
①当上底AD是7时,如图
过A作AE⊥BC于E,过D作DF⊥BC于F,
则AE∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∵∠AEF=90°,
∴平行四边形AEFD是矩形,
∴AD=EF=7,AE=DF=12,
在Rt△ABE和Rt△DFC中,由勾股定理得:BE=
=9,CF=
=16,
∴BC=9+7+16=32(cm);
②当下底BC=7时,如图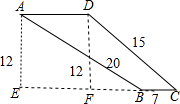
过A作AE⊥CB,交CB的延长线于E,过D作DF⊥CB,交CB的延长线于F,
则AE∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∵∠AEF=90°,
∴平行四边形AEFD是矩形,
∴AD=EF,AE=DF=12,
在Rt△ABE和Rt△DFC中,由勾股定理得:CF=
=9,BE=
=16,
∴AD=EF=BE-(CF-CB)=16-(9-7)═14(cm)
故答案为32cm或14cm.
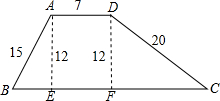
①当上底AD是7时,如图
过A作AE⊥BC于E,过D作DF⊥BC于F,
则AE∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∵∠AEF=90°,
∴平行四边形AEFD是矩形,
∴AD=EF=7,AE=DF=12,
在Rt△ABE和Rt△DFC中,由勾股定理得:BE=
| 152-122 |
| 202-122 |
∴BC=9+7+16=32(cm);
②当下底BC=7时,如图

过A作AE⊥CB,交CB的延长线于E,过D作DF⊥CB,交CB的延长线于F,
则AE∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∵∠AEF=90°,
∴平行四边形AEFD是矩形,
∴AD=EF,AE=DF=12,
在Rt△ABE和Rt△DFC中,由勾股定理得:CF=
| 152-122 |
| 202-122 |
∴AD=EF=BE-(CF-CB)=16-(9-7)═14(cm)
故答案为32cm或14cm.


练习册系列答案
相关题目


 的中点.
的中点.