��Ŀ����
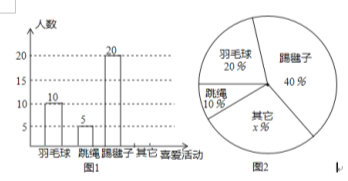
����Ŀ����������ֻ�Խ��Խ�ռ����кܶ��˿�ʼ���������ֻ���һ����ʹ���ֻ�ʱ��������γ��ˡ��ֻ���Ϊ�˽���У�����꼶ѧ�����ֻ�ʹ�������ѧ������������˲���ѧ�����ֻ�ʹ��ʱ�䣬���������ֳ����ࣺA���������ã�B��ƽ��һ��ʹ��1��2Сʱ��C��ƽ��һ��ʹ��2��4Сʱ��D��ƽ��һ��ʹ��4��6Сʱ��E��ƽ��һ��ʹ�ó���6Сʱ�����õõ������ݻ��Ƴ�������������������ͳ��ͼ��ͼ1��2��������������Ϣ������������⣺ 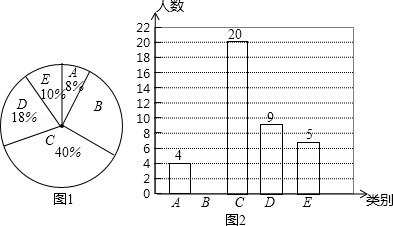
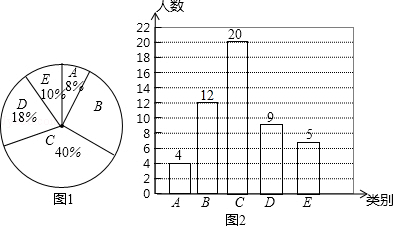
��1�������������ͳ��ͼ����������
��2����һ�����ֻ�ʹ��ʱ�䳬��6Сʱ���������صġ��ֻ�����У�����꼶����1490�ˣ��Թ�����У�����꼶��Լ�ж����˻������صġ��ֻ���
��3���ڱ�����Ļ��������ֻ���4λͬѧ����2��2Ů����Ҫ��������ٳ�����ͬѧȥ�μ���̸���������б�������״ͼ���������ѡ��λͬѧǡ����һ����ͬѧ��һλŮͬѧ�ĸ��ʣ�
���𰸡�
��1���⣺��������ã�20��40%=50���ˣ���
��B�������Ϊ50����4+20+9+5��=12���ˣ���
��ȫ����ͳ��ͼ����ͼ��ʾ��
 ��
��
��2���⣺��������ã� ![]() ��1490=149���ˣ���
��1490=149���ˣ���
����У�����꼶��Լ��149�˻������صġ��ֻ���
��3���⣺�б����£�
�� | �� | ٠| ٠| |
�� | ������ | ���У��У� | ��Ů���У� | ��Ů���У� |
�� | ���У��У� | ������ | ��Ů���У� | ��Ů���У� |
Ů | ���У�Ů�� | ���У�Ů�� | ������ | ��Ů��Ů�� |
Ů | ���У�Ů�� | ���У�Ů�� | ��Ů��Ů�� | ������ |
���еȿ��ܵ������12�֣�������ѡ��λͬѧǡ����һ����ͬѧ��һλŮͬѧ�������8�֣�
��P��һ��һŮ��= ![]() =
= ![]() ��
��
����������1������C�������������ռ�İٷֱ����������������ȷ����B�����������ȫ����ͳ��ͼ���ɣ���2���������������һ�����ֻ�ʹ��ʱ�䳬��6Сʱ��ռ�İٷֱȣ�����1490���ɵõ��������3���б��ó����еȿ��ܵ���������ҳ���ѡ��λͬѧǡ����һ����ͬѧ��һλŮͬѧ��������������������ʣ�

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�