Question

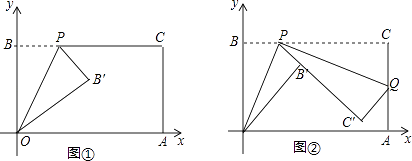
【题目】如图1，抛物线y=ax2+bx+3（a≠0）与x轴、y轴分别交于点A（﹣1，0）、B（3，0）、点C三点．

（1）试求抛物线的解析式；
（2）点D（2，m）在第一象限的抛物线上，连接BC、BD．试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由；
（3）如图2，在（2）的条件下，将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，记平移后的三角形为△B′O′C′．在平移过程中，△B′O′C′与△BCD重叠的面积记为S，设平移的时间为t秒，试求S与t之间的函数关系式？

Answer 1

【答案】
（1）

解：将A（﹣1，0）、B（3，0）代入抛物线y=ax2+bx+3（a≠0），

，

解得：a=﹣1，b=2．

故抛物线解析式为：y=﹣x2+2x+3．

（2）

解：存在

将点D代入抛物线解析式得：m=3，

∴D（2，3），

令x=0，y=3，

∴C（0，3），

∴OC=OB，

∴∠OCB=∠CBO=45°，

如下图，

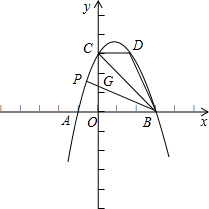
在y轴上取点G，使GC=CD=2，

在△CDB与△CGB中

∵BC=BC、∠DCB=∠BCO、GC=DC（SAS）

∴△CDB≌△CGB，

∴∠PBC=∠DBC，

∵点G（0，1），

设直线BP：y=kx+1，

代入点B（3，0），

∴k=﹣ ，

∴直线BP：y=﹣ x+1，

联立直线BP和二次函数解析式：

，

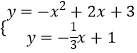解得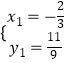： 或 （舍），

∴P（﹣ ， ）．

（3）

解：直线BC：y=﹣x+3，直线BD：y=﹣3x+9，

当0≤t≤2时，如下图：

设直线C′B′：y=﹣（x﹣t）+3

联立直线BD求得F（ ， ），

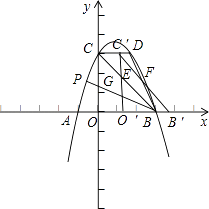
S=S△BCD﹣S△CC′E﹣S△C′DF

= ×2×3﹣ ×t×t﹣ ×（2﹣t）（3﹣ ）

整理得：S=﹣ t2+3t（0≤t≤2）．

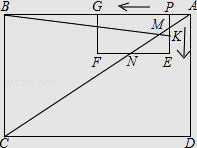
当2＜t≤3时，如下图：

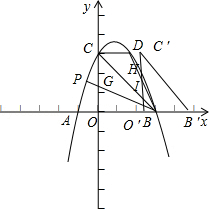
H（t，﹣3t+9），I（t，﹣t+3）

S=S△HIB= [（﹣3t+9）﹣（﹣t+3）]×（3﹣t）

整理得：S=t2﹣6t+9（2＜t≤3）

综上所述：S= ．

【解析】（1）将点A、B代入抛物线解析式，求出a、b值即可得到抛物线解析式；（2）根据已知求出点D的坐标，在y轴上取点G，使GC=CD=2，只要证明证明△CDB≌△CGB，可知∠PBC=∠DBC，写出直线BP解析式，联立二次函数解析式，求出点P坐标；（3）分两种情况，第一种情况重叠部分为四边形，利用大三角形减去两个小三角形求得解析式，第二种情况重叠部分为三角形，可利用三角形面积公式求得．
【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．