题目内容
如图,∠BAC=45º,AD⊥BC于点D,且BD=3,CD=2,则AD的长为 .

6.
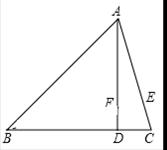
试题分析:如 图,过B作BE⊥AC,垂足为E交AD于F,由∠BAC=45°可以得到BE=AE,再根据已知条件可以证明△AFE≌△BCE,可以得到 AF=BC=10,而∠FBD=∠DAC,又∠BDF=∠ADC=90°,由此可以证明△BDF∽△ADC,所以FD:DC=BD:AD,设FD长为x,则可建立关于x的方程,解方程即可求出FD,AD的长.
试题解析:如图,过B作BE⊥AC,垂足为E交AD于F
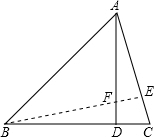
∵∠BAC=45°
∴BE=AE,
∵∠C+∠EBC=90°,∠C+∠EAF=90°,
∴∠EAF=∠EBC,
在△AFE与△BCE中,
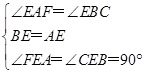 ,
,∴△AFE≌△BCE(ASA)
∴AF=BC=BD+DC=10,∠FBD=∠DAC,
又∵∠BDF=∠ADC=90°
∴△BDF∽△ADC
∴FD:DC=BD:AD
设FD长为x
即x:2=3:(x+5)
解得x=1
即FD=1
∴AD=AF+FD=5+1=6.
考点: 1.相似三角形的判定与性质;2.解一元二次方程-公式法;3.全等三角形的判定与性质.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
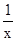 图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
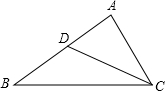
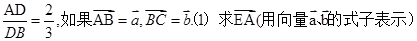 ;(2)求作向量
;(2)求作向量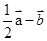 (不要求写作法,但要指出所作图中表示结论的向量)。
(不要求写作法,但要指出所作图中表示结论的向量)。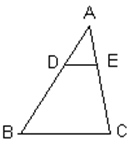
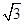 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.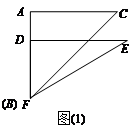
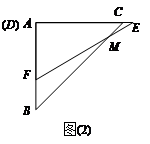
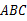 中,
中,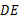 ∥
∥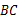 ,
,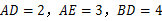 ,则
,则 ______.
______.