题目内容
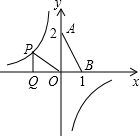
平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=﹣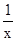 图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
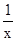 图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
D
可以分别从△PQO∽△AOB与△PQO∽△BOA去分析,首先设点P(x,y),根据相似三角形的对应边成比例与反比例函数的解析式,联立可得方程组,解方程组即可求得点P的坐标,即可求得答案.
解:∵点P在反比例函数y=﹣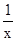 图象上,
图象上,
∴设点P(x,y),
当△PQO∽△AOB时,则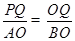 ,
,
又PQ=y,OQ=﹣x,OA=2,OB=1,
即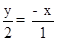 ,即y=﹣2x,
,即y=﹣2x,
∵xy=﹣1,即﹣2x2=﹣1,
∴x=±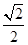 ,
,
∴点P为(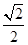 ,﹣
,﹣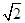 )或(﹣
)或(﹣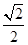 ,
,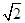 );
);
同理,当△PQO∽△BOA时,
求得P(﹣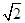 ,
,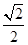 )或(
)或(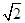 ,﹣
,﹣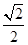 );
);
故相应的点P共有4个.
故选D.
解:∵点P在反比例函数y=﹣
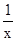 图象上,
图象上,∴设点P(x,y),
当△PQO∽△AOB时,则
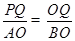 ,
,又PQ=y,OQ=﹣x,OA=2,OB=1,
即
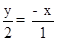 ,即y=﹣2x,
,即y=﹣2x,∵xy=﹣1,即﹣2x2=﹣1,
∴x=±
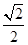 ,
,∴点P为(
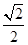 ,﹣
,﹣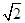 )或(﹣
)或(﹣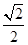 ,
,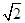 );
);同理,当△PQO∽△BOA时,
求得P(﹣
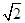 ,
,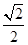 )或(
)或(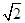 ,﹣
,﹣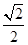 );
);故相应的点P共有4个.
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
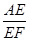 =3,求
=3,求 的值.
的值.
 =a,
=a, =b(a>0,b>0)则
=b(a>0,b>0)则