题目内容
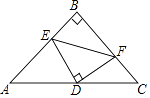
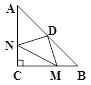
【题目】在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )
A. ①②④; B. ①②③; C. ②③④; D. ①②③④.
【答案】D
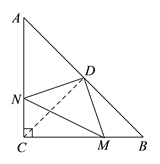
【解析】连接CD,
∵在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,
∴∠B=∠NCD=45°,CD=BD,∠CDB=90°,S△CDB=![]() S△ABC=
S△ABC=![]() ·
·![]() AC·BC=
AC·BC=![]() =4 ,
=4 ,
又∵BM=CN,
∴△DBM≌△DCN,
∴DN=DM,∠CDN=∠DBM,S△CDN=S△DBM,
∴∠DMN=∠CDN+∠CDM=∠CDM+∠BDM=∠CDB=90°,
S四边形CMDN=S△CDN+S△CDM= S△BDM+S△CDM=S△CBD=4.
∵S△CMN+S△DMN= S四边形CMDN=4,
∴当S△DMN最小时,S△CMN的面积最大,
∴当DM⊥BC时,DM=DN=2,此时S△DMN最小=2,
∴此时,S△CMN的面积最大=4-2=2.
综上所述,上述四个结论全都正确.
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目