��Ŀ����
����Ŀ����ͼ����M������ABCD��ƽ��ֱ������ϵ�У���M������Ϊ����3��1������A������Ϊ��2��0������B������Ϊ��1���� ![]() ������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
��1��������ABCD���ܳ���
��2������M��x��������ÿ��2����λ���ȵ��ٶ�ƽ�ƣ�����ABCD��x��������ÿ��3����λ���ȵ��ٶ�ƽ�ƣ��������ƶ���ʱ��Ϊt���룩������M��AD���У����е�ΪAD���е�ʱ������AC����t��ֵ����MAC�Ķ�����
��3���ڣ�2���������£�����M��AC���ڵ�ֱ�ߵľ���Ϊ1ʱ����t��ֵ��
���𰸡�
��1���⣺����B��BE��AD������ΪE��
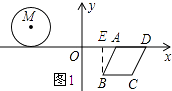
��B��1���� ![]() ����A��2��0����
����A��2��0����
��BE= ![]() ��AE=1��
��AE=1��
��AB= ![]() =2��
=2��
���ı���ABCDΪ���Σ�
��AB=BC=CD=AD��
�����ε��ܳ�=2��4=8��
��2���⣺��ͼ2��ʾ����M��x�������ΪF��AD���е�ΪE��
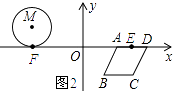
��M����3��1����
��F����3��0����
��AD=2����EΪAD���е㣬
��E��3��0����
��EF=6��
��2t+3t=6��
��ã�t= ![]() ��
��
ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ��M��AD���е㣮
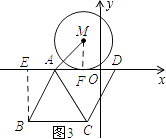
���ɣ�1����֪��AE=1��BE= ![]() ��
��
��tan��EAB= ![]() ��
��
���EAB=60�㣮
���FAB=120�㣮
���ı���ABCD�����Σ�
���FAC= ![]() ��FAB=
��FAB= ![]() ��120��=60�㣮
��120��=60�㣮
��ADΪ��M�����ߣ�
��MF��AD��
��FΪAD���е㣬
��AF=MF=1��
���AFMΪ����ֱ�������Σ�
���MAF=45�㣮
���MAC=��MAF+��FAC=45��+60��=105�㣮
��3���⣺��ͼ4��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE��
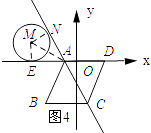
���ı���ABCDΪ���Σ���DAB=120�㣬
���DAC=60�㣮
��AC��AD��ԲM�����ߣ�
���MAE=30�㣮
��ME=MN=1��
��EA= ![]() ��
��
��3t+2t=5�� ![]() ��
��
��t=1�� ![]() ��
��
��ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE��
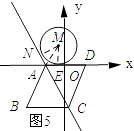
���ı���ABCDΪ���Σ���DAB=120�㣬
���DAC=60�㣮
���NAE=120�㣮
��AC��AD��ԲM�����ߣ�
���MAE=60�㣮
��ME=MN=1��
��EA= ![]() ��
��
��3t+2t=5+ ![]() ��
��
��t=1+ ![]() ��
��
����������t=1�� ![]() ��t=1+
��t=1+ ![]() ʱ��ԲM��AC���У�
ʱ��ԲM��AC���У�
����������1������B��BE��AD������ΪE����A��B��������ɶ��������AB�ij��������ɵ�����ABCD���ܳ���
��2�����M��x�������ΪF��AD���е�ΪE.�������������EF�ij����Ӷ����t��ֵ������B��BE��AD������ΪE������MF��FΪ��M��AD���е㣮����AD��ԲM�����ߺ����ε����ʣ���֤�á�AFMΪ����ֱ�������Σ��Ӷ���á�MAC�Ķ�����
��3����ͼ4��ͼ5�У�����AM��������MN��AC������ΪN����ME��AD������ΪE��ͼ4�У����ı���ABCDΪ���Σ��ɵá�DAC=60�㣬����AC��AD��ԲM�����ߣ��ɵá�MAE=30�㣬�����Ǻ����ɵ�EA�ij�������3t+2t=5-AE�����t��ֵ��ͼ5�У�ͬ�������AEden��������3t+2t=5+AE���t��ֵ.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�