题目内容
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)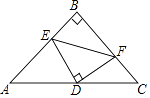
【答案】( ![]() m+2)
m+2)
【解析】解:如图,
连接BD,在等腰Rt△ABC中,点D是AC的中点,
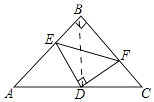
∴BD⊥AC,
∴BD=AD=CD,∠DBC=∠A=45°,∠ADB=90°,
∵∠EDF=90°,
∴∠ADE=∠BDF,
在△ADE和△BDF中, 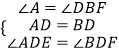 ,
,
∴△ADE≌△BDF(ASA),
∴AE=BF,DE=DF,
在Rt△DEF中,DF=DE=m.
∴EF= ![]() DE=
DE= ![]() m,
m,
∴△BEF的周长为BE+BF+EF=BE+AE+EF=AB+EF=2+ ![]() m,
m,
所以答案是:( ![]() m+2)
m+2)
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
【题目】某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )
包场计费:包场每场每小时50元,每人须另付入场费5元 |
人数计费:每人打球2小时20元,接着续打球每人每小时6元 |
A. 9B. 8C. 7D. 6