题目内容
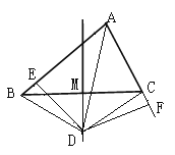
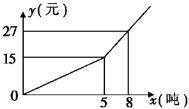
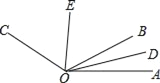
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
【答案】(1) 65°’;(2) 150°;(3) ∠DOE=![]() ∠AOC,理由见解析
∠AOC,理由见解析
【解析】
(1)利用角平分线的定义得出∠AOD=∠BOD,∠BOE=∠COE,进而求出∠DOE的度数;
(2)根据角平分线的定义求出∠DOB和∠EOB的度数,代入∠DOE=∠DOB+∠EOB求出即可;
(3)根据角的和差关系求出∠AOC度数,再根据角平分线的定义求出∠DOB和∠EOB,代入∠DOE=![]() ∠BOC+∠AOB得出关系即可.
∠BOC+∠AOB得出关系即可.
(1)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∵∠BOC=50°,∠BOA=80°,
∴∠BOD=25°,∠BOE=40°,
∴∠DOE=25°+40°=65°;
(2)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∵∠AOC=150°,
∴∠DOE=∠DOB+∠EOB=![]() (∠BOC+∠BOA)=
(∠BOC+∠BOA)=![]() ∠AOC=75°;
∠AOC=75°;
(3)∠DOE=![]() ∠AOC;
∠AOC;
理由是:∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∴∠DOE=∠DOB+∠EOB=![]() (∠BOC+∠BOA)=
(∠BOC+∠BOA)=![]() ∠AOC.
∠AOC.

练习册系列答案
相关题目