题目内容
【题目】如图,在平面直角坐标系中,A(0,2![]() ),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )
),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )

A. ![]() B.
B. ![]() C. 4
C. 4![]() +6 D. 4
+6 D. 4![]() -6
-6
【答案】C
【解析】分析:如图所示,根据题意画出图形,并作矩形OGEF,先证Rt△AOB≌Rt△BEA,再证△BEF是含有30°角的三角形,从而求出BF与EF的长,最后在Rt△AGE中利用勾股定理建立含t的方程,解方程即可得出答案.
详解:当点B运动到如图所示的位置时,⊙A与边BD所在直线相切,切点为E,
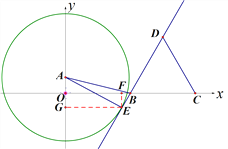
作EF⊥x轴,垂足为F,作EG⊥y轴,垂足为G,可得矩形OGEF,
在Rt△AOB与Rt△BEA中,
![]()
∴Rt△AOB≌Rt△BEA,
∴BE=AO=2![]() ,
,
∵△BCD是等边三角形,
∴∠DBC=60°,
∴∠FBE=∠DBC=60°,
∵∠BFE=90°,
∴∠BEF=30°,
∴BF=![]() ,EF=3,
,EF=3,
∴GE=t-![]() ,AG=2
,AG=2![]() +3,
+3,
在Rt△AGE中,由勾股定理得,
AG2+GE2=AE2,
即![]() ,
,
解得,![]() .
.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






