ЬтФПФкШн
ЁОЬтФПЁПдФЖСЯТСаВФСЯНтОіЮЪЬтЃКСНИіЖрЮЛЪ§ећЪ§ЃЌШєЫќУЧИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЯрЕШЃЌдђГЦетСНИіЖрЮЛЪ§ЛЅЮЊЁАЕїКЭЪ§ЁБЃЌР§Шч37КЭ82ЃЌЫќУЧИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЗжБ№ЮЊ3+7КЭ8+2ЃЌЯдШЛ3+7ЃН8+2ЃН10ЙЪ37КЭ82ЛЅЮЊЁАЕїКЭЪ§ЁБЃЎ
ЃЈ1ЃЉЯТСаЫЕЗЈДэЮѓЕФЪЧЁЁ ЁЁ
A.123КЭ51ЛЅЮЊЕїКЭЪ§ЁБ ЃЛ B.345КЭ513ЛЅЮЊЁАЕїКЭЪ§ЃЛ C.2018КЭ8120ЛЅЮЊЁАЕїКЭЪ§ЁБЃЛ DЃЎСНЮЛЪ§![]() КЭ
КЭ![]() ЛЅЮЊЁАЕїКЭЪ§ЁБ
ЛЅЮЊЁАЕїКЭЪ§ЁБ
ЃЈ2ЃЉШєAЁЂBЪЧСНИіВЛЕШЕФСНЮЛЪ§ЃЌAЃН![]() ЃЌBЃН
ЃЌBЃН![]() ЃЌAКЭBЛЅЮЊЁАЕїКЭЪ§ЁБЃЌЧвAгыBжЎКЭЪЧBгыAжЎВюЕФ3БЖЃЌЧѓжЄЃКy=-x+9.
ЃЌAКЭBЛЅЮЊЁАЕїКЭЪ§ЁБЃЌЧвAгыBжЎКЭЪЧBгыAжЎВюЕФ3БЖЃЌЧѓжЄЃКy=-x+9.
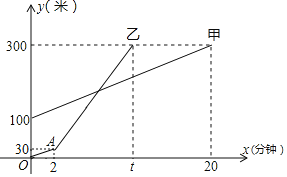
ЁОД№АИЁПЃЈ1ЃЉBЃЛЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌСНИіЖрЮЛЪ§ећЪ§ЃЌШєЫќУЧИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЯрЕШЃЌдђГЦетСНИіЖрЮЛЪ§ЛЅЮЊЁАЕїКЭЪ§ЁБЃЌМДПЩзїД№
ЃЈ2ЃЉЯШгУЁАЕїКЭЪ§ЁБЃЌЕУГіx+y=m+nЃЌдйРћгУAгыBжЎКЭЪЧBгыAжЎВюЕФ3БЖЃЌЕУГіx+y=9(m-2x)ЃЌдђx+yЪЧ9ЕФБЖЪ§ЃЛЕУГіНсТлГЩСЂ.
НтЃКЃЈ1ЃЉИљОнЕїКЭЪ§ЕФЖЈвхЃЌЭЈЙ§МЦЫуИїЮЛЪ§жЎКЭЃЌвзжЊBбЁЯюДэЮѓ
ЙЪбЁдёЃКBЃЛ
ЃЈ2ЃЉжЄУїЃКгаЬтвтПЩжЊЃК![]() ЃЌ
ЃЌ
Ыљвдx+y=9(m-2x)ЃЌдђx+yЪЧ9ЕФБЖЪ§ЃЛ
Ыљвдx+y=9Лђ18ЃЛ
Ыљвдy=-x+9.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПЯТБэЪЧФГжабЇЦпФъМЖ5УћбЇЩњЕФЬхжиЧщПіЃК
аеУћ | аЁгБ | аЁУї | аЁИе | аЁОЉ | аЁФў |
ЬхжиЃЈЧЇПЫЃЉ | 34 | 45 | |||
ЬхжигыЦНОљЬхжиЕФВю | -6 | +3 | -4 | 0 |
ЃЈ1ЃЉЭъГЩЩЯБэ.
ЃЈ2ЃЉЫзюжиЃПЫзюЧсЃП
ЃЈ3ЃЉзюжиЕФгызюЧсЕФЯрВюЖрЩйЃП