题目内容
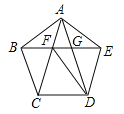
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

【答案】(1)见解析;(2)见解析;(3)![]() +1
+1
【解析】分析:(1)由题意得,∠BAE=∠EAG,∠DAF=∠FAG,于是得到∠BAD=2∠EAF=90°,推出四边形ABCD是矩形,根据正方形的判定定理即可得到结论;
(2)根据EG=BE,FG=DF,得到EF=BE+DF,于是得到△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD,即可得到结论;
(3)根据EC=FC=1,得到BE=DF,根据勾股定理得到EF=![]() ,于是得到结论.
,于是得到结论.
详(1)证明:由题意得,∠BAE=∠EAG,∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°,
∴四边形ABCD是矩形,
∵AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)证明:∵EG=BE,FG=DF,
∴EF=BE+DF,
∴△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD,
∴三角形ECF的周长是四边形ABCD周长的一半;
(3)∵EC=FC=1,
∴BE=DF,
∴EF=![]() ,
,
∵EF=BE+DF,
∴BE=DF=![]() EF=
EF=![]() ,
,
∴AB=BC=BE+EC=![]() +1.
+1.

练习册系列答案
相关题目