题目内容
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C 在数轴上表示的数是10.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 .(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式![]() ,若存在,求线段PD的长;若不存在,请说明理由.
,若存在,求线段PD的长;若不存在,请说明理由.
【答案】(1)-6+6t;10+2t;(2)![]() ,
,![]() ;(3)PD=
;(3)PD=![]() 或
或![]()
【解析】
(1)根据题意列出代数式即可.
(2)根据题意分点B在点C左边和右边两种情况,列出方程解出即可.
(3)随着点B的运动大概,分别讨论当点B和点C重合、点C在A和B之间及点A与点C重合的情况.
(1)点B表示的数是-6+6t;
点C表示的数是10+2t.
(2)![]()
![]() 或
或![]()
∴![]() 或
或 ![]()
(3)设未运动前P点表示的数是x,
则运动t 秒后,A点表示的数是![]()
B点表示的数是-6+6t
C点表示的数是10+2t
D点表示的数是14+2t
P点表示的数是x+6t
则BD=14+2t-(-6+6t)=20-4t
AP=x+6t-(-8+6t)=x+8
PC=![]() (P点可能在C点左侧,也可能在右侧)
(P点可能在C点左侧,也可能在右侧)
PD=14+2t-(x+6t)=14-(4t+x)
∵![]()
∴20-4t-(x+8)=4![]()
∴12-(4t+x)=4(4t+x)-40 或 12-(4t+x)=40-4(4t+x)
∴4t+x=![]() 或 4t+x=
或 4t+x=![]()
∴PD=14+2t-(x+6t)=14-(4t+x)=![]() 或
或![]() .
.

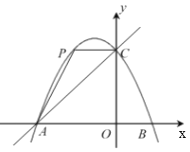
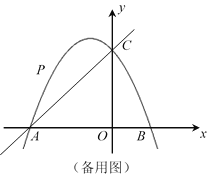
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的