题目内容
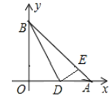
【题目】如图,在平面直角坐标系中,![]() 为线段
为线段![]() 上任一点,作
上任一点,作![]() 交线段
交线段![]() 于
于![]() ,当
,当![]() 的长最大时,点
的长最大时,点![]() 的坐标为_________.
的坐标为_________.
【答案】(3,![]() )
)
【解析】
根据勾股定理求出AB,由DE⊥BD,取BE的中点F,以点F为圆心,BF长为半径作半圆,与x轴相切于点D,连接FD,设AE=x,利用相似三角形求出x,再根据三角形相似求出点E的横纵坐标即可.
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=5,
∵DE⊥BD,
∴∠BDE=90°,
取BE的中点F,以点F为圆心,BF长为半径作半圆,与x轴相切于点D,连接FD,
设AE=x,则BF=EF=DF=![]() ,
,
∵∠ADF=∠AOB=90°,
∴DF∥OB
∴△ADF∽△AOB
∴![]()
∴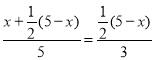 ,
,
解得x=![]() ,
,
过点E作EG⊥x轴,
∴EG∥OB,
∴△AEG∽△ABO,
∴![]() ,
,
∴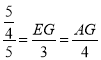 ,
,
∴EG=![]() ,AG=1,
,AG=1,
∴OG=OA-AG=4-1=3,
∴E(3,![]() ),
),
故答案为:(3,![]() ).
).

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目