题目内容
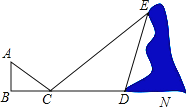
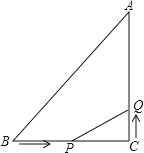
【题目】如图,△ABC 中,∠C=90°,AC=3cm,BC=4cm,动点 P 从点 B 出发以 2cm/s 速度向点 c 移动,同时动点 Q 从 C 出发以 1cm/s 的速度向点 A 移动, 设它们的运动时间为 t.
(1)根据题意知:CQ= ,CP= ;(用含 t 的代数式表示)
(2)t 为何值时,△CPQ 的面积等于△ABC 面积的![]() ?
?
(3)运动几秒时,△CPQ 与△CBA 相似?
【答案】(1)PC=4﹣2t,CQ=t(2)经过![]() 或
或![]() 秒后,△CPQ 的面积等于△ABC 面积的
秒后,△CPQ 的面积等于△ABC 面积的![]() (3)1.2 或
(3)1.2 或![]()
【解析】
(1)由动点 P 从点 B 出发以 2cm/s 速度向点 c 移动,同时动点 Q 从 C 出发以 1cm/s 的速度向点 A 移动, 设它们的运动时间为 t,可得PC为4﹣2t,CQ为t;
(2)由△CPQ 的面积等于△ABC 面积的![]() ,可列方程
,可列方程![]() (4-2t)
(4-2t)![]() t=
t= ![]() ×
×![]() ×3×4,求出t的值即可;
×3×4,求出t的值即可;
(3)分Rt△ABC∽Rt△QPC与Rt△ABC∽Rt△PQC两种情况讨论,有对应边成比例,可求得t的值.
(1)经过t秒后,PC=4﹣2t,CQ=t,
(2)当△CPQ 的面积等于△ABC面积的![]() 时,即
时,即![]() (4-2t)
(4-2t)![]() t=
t= ![]() ×
×![]() ×3×4,
×3×4,
解得;t=![]() 或 t=
或 t=![]() ;
;
答:经过![]() 或
或![]() 秒后,△CPQ 的面积等于△ABC 面积是
秒后,△CPQ 的面积等于△ABC 面积是![]() ;
;
(3)设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①若 Rt△ABC∽Rt△QPC 则![]() =
=![]() ,即
,即![]() =
=![]() ,解得 t=1.2;
,解得 t=1.2;
②若 Rt△ABC∽Rt△PQC 则![]() =
=![]() ,即
,即![]() =
=![]() ,解得 t=
,解得 t=![]() ;
;
由 P 点在 BC 边上的运动速度为 2cm/s,Q 点在 AC 边上的速度为 1cm/s,可求出t 的取值范围应该为 0<t<2,
验证可知①②两种情况下所求的 t 均满足条件.
答:要使△CPQ 与△CBA 相似,运动的时间为 1.2 或![]() 秒.
秒.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案