题目内容
【题目】台州人民翘首以盼的乐清湾大桥于2018年9月28日正式通车，经统计分析，大桥上的车流速度
（千米/小时）是车流密度
（辆/千米）的函数，当桥上的车流密度达到220辆/千米的时候就造成交通堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米，车流速度为80千米/小时，研究证明：当
时，车流速度是车流密度的一次函数．
（1）求大桥上车流密度为50/辆千米时的车流速度；
（2）在某一交通高峰时段，为使大桥上的车流速度大于60千米/小时且小于80千米/小时，应把大桥上的车流密度控制在什么范围内？
（3）车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量
车流速度
车流密度，求大桥上车流量
的最大值．
【答案】（1）车流速度68千米/小时；（2）应把大桥上的车流密度控制在20千米/小时到70千米/小时之间；（3）车流量y取得最大值是每小时4840辆
【解析】
（1）设车流速度
与车流密度
的函数关系式为v=kx+b，列式求出函数解析式，将x=50代入即可得到答案；
（2）根据题意列不等式组即可得到答案；
（3）分两种情况：
、
时分别求出y的最大值即可.
（1）设车流速度与车流密度的函数关系式为v=kx+b，由题意，得
，
解得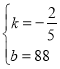
，
∴当时，车流速度是车流密度的一次函数为
，
当x=50时，
（千米/小时），
∴大桥上车流密度为50/辆千米时的车流速度68千米/小时；
（2）由题意得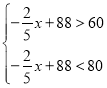
，
解得20<x<70，符合题意，
∴为使大桥上的车流速度大于60千米/小时且小于80千米/小时，应把大桥上的车流密度控制在20千米/小时到70千米/小时之间；
（3）由题意得y=vx，
当时，y=80x，
∵k=80>0，
∴y随x的增大而增大，
∴当x=20时，y有最大值1600，
当时，
y
，
当x=110时，y有最大值4840，
∵4840>1600，
∴当车流密度是110辆/千米，车流量y取得最大值是每小时4840辆.
