题目内容
【题目】如图,AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,点D′落在AC上,C′D′交BC于点E,若AB=1,则图中阴影部分图形的面积是 . 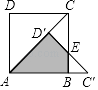
【答案】![]() ﹣1
﹣1
【解析】解:∵AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,
∴∠ACB=∠BC′E=45°,AD′=AD=AB=1,AC= ![]() ,∠CD′C′=90°,
,∠CD′C′=90°,
∴S阴影=S△ABC﹣S△ECD′= ![]() ×1×1﹣
×1×1﹣ ![]() ×(
×( ![]() ﹣1)×(
﹣1)×( ![]() ﹣1)=
﹣1)= ![]() ﹣1.
﹣1.
故答案是: ![]() .
.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目