题目内容
【题目】如图，在矩形ABCD中，AB=4cm，BC=3cm，动点P从点A出发，沿AB以1cm/s的速度向终点B匀速运动，同时点Q从点B出发，沿B→C→D以1cm/s的速度向终点D匀速运动，当两个点中有一个到达终点后，另一个点也随之停止．连接PQ，设点P的运动时间为x（s），PQ2=y（cm2）．
（1）当点Q在边CD上，且PQ=3时，求x的值；
（2）求y与x之间的函数关系式，并写出自变量x的取值范围；
（3）直接写出y随x增大而增大时自变量x的取值范围．
【答案】
（1）
解：如图①中，
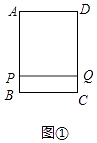
当点Q在边CD上时，且PQ=AD=3，则PQ∥BC，四边形PBCQ是矩形，
∴PB=CQ，
∴4﹣x=x﹣3，
∴x=3.5
（2）
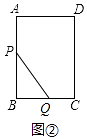
解：如图②中，
当0≤x≤3时，y=（4﹣x）2+x2=2x2﹣8x+16．
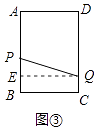
如图③中，当3＜x≤4时，过点Q作QE⊥AB于点E，则QE=3，
y=（7﹣2x）2+32=4x2﹣28x+58．
（3）
解：∵当0≤x≤3时，y=2x2﹣8x+16=2（x﹣2）2+8．
当3＜x≤4时，y=4x2﹣28x+58=4（x﹣ 
）2+9．
∴当2≤x≤3或 
x≤4时，y随x增大而增大
【解析】（1）根据条件可知四边形PBCQ是矩形，推出PB=CQ，列出方程即可解决问题．（2）分两种情形①如图②中，当0≤x≤3时，②如图③中，当3＜x≤4时，过点Q作QE⊥AB于点E，分别利用勾股定理即可解决问题．（3）把（2）中的二次函数，利用配方法，求出对称轴，即可判断．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
练习册系列答案
相关题目
