��Ŀ����
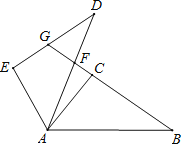
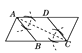
����Ŀ������ԭ�ͣ���ͼ�٣��ڵ���ֱ��������ABC�У���ACB=90�㣬BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE��
��֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ ![]() ��
��
����̽������ͼ�ڣ���Rt��ABC�У���ACB=90�㣬BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
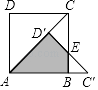
��Ӧ�ã���ͼ�ۣ��ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
���𰸡��⣺����̽������BCD�����Ϊ ![]() ��
��
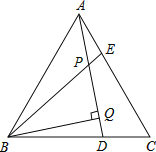
���ɣ���ͼ�ڣ�����D��BC�Ĵ��ߣ���BC���ӳ��߽��ڵ�E��
���BED=��ACB=90�㣮
���߶�AB�Ƶ�B˳ʱ����ת90��õ��߶�BE��
��AB=BD����ABD=90�㣮
���ABC+��DBE=90�㣮
�ߡ�A+��ABC=90�㣮
���A=��DBE��
�ڡ�ABC�͡�BDE�У� ��
��
���ABC�ա�BDE��AAS��
��BC=DE=a��
��S��BCD= ![]() BCDE
BCDE
��S��BCD= ![]() ��
��
��Ӧ�ã���ͼ�ۣ�����A��AF��BC��F������D��DE��BC���ӳ����ڵ�E��
���AFB=��E=90�㣬BF= ![]() BC=
BC= ![]() a��
a��
���FAB+��ABF=90�㣮
�ߡ�ABD=90�㣬
���ABF+��DBE=90�㣬
���FAB=��EBD��
���߶�BD�����߶�AB��ת�õ��ģ�
��AB=BD��
�ڡ�AFB�͡�BED�У�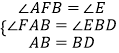 ��
��
���AFB�ա�BED��AAS����
��BF=DE= ![]() a��
a��
��S��BCD= ![]() BCDE��
BCDE��
��S��BCD= ![]()
![]() aa=
aa= ![]() a2 ��
a2 ��
���BCD�����Ϊ ![]() ��
��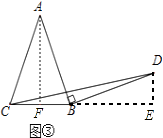
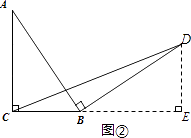
������������̽������ͼ�ڣ�����D��BC�Ĵ��ߣ���BC���ӳ��߽��ڵ�E���ɴ�ֱ�����ʾͿ��Եó���ABC�ա�BDE������DE=BC=a�������������ε������ʽ�ó����ۣ�
�����ã���ͼ�ۣ�����A��AF��BC��F������D��DE��BC���ӳ����ڵ�E���ɵ��������ε����ʿ��Եó�BF= ![]() BC�����������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE���������ε������ʽ�Ϳ��Եó����ۣ�
BC�����������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE���������ε������ʽ�Ϳ��Եó����ۣ�