Question

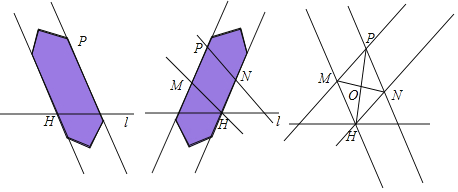
【题目】如图：在△ABC中，∠C=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于M，BN⊥MN于N．

(1)MN=AM+BN成立吗？为什么？

(2)若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之间有什么关系？请说明理由．

Answer 1

【答案】（1）MN=AM+BN成立，理由见解析；（2）MN＝BNAM，理由见解析.

【解析】

（1）利用同角的余角相等证明∠MAC＝∠NCB，由∠AMC＝∠CNB＝90°，AC＝BC，可证△AMC≌△CNB，从而有AM＝CN，MC＝BN，即可得出结论；

（2）类似于（1）的方法，证明△AMC≌△CNB，从而有AM＝CN，MC＝BN，可推出AM、BN与MN之间的数量关系．

解：（1）MN=AM+BN成立；

理由：∵AM⊥MN，BN⊥MN，

∴∠AMC＝∠CNB＝90°，

∵∠ACB＝90°，

∴∠MAC＋∠ACM＝90°，∠NCB＋∠ACM＝90°，

∴∠MAC＝∠NCB，

在△AMC和△CNB中，，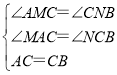

∴△AMC≌△CNB（AAS），

∴AM＝CN，MC＝BN，

∵MN＝CN＋MC，

∴MN＝AM＋BN；

（2）MN＝BNAM．

理由：∵AM⊥MN，BN⊥MN，

∴∠AMC＝∠CNB＝90°，

∵∠ACB＝90°，

∴∠MAC＋∠ACM＝90°，∠NCB＋∠ACM＝90°，

∴∠MAC＝∠NCB，

在△AMC和△CNB中，，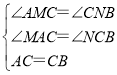

∴△AMC≌△CNB（AAS），

∴AM＝CN，MC＝BN，

∵MN＝MCCN，

∴MN＝BNAM．