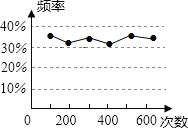
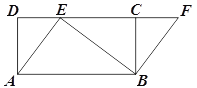
题目内容
【题目】如图,双边直尺有两条平行的边,但是没有刻度,可以用来画等距平行线:
![]()
我们也可用工具自制(如图):
![]()
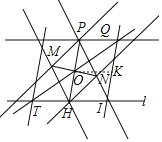
下面是小My同学设计的“过直线外一点作这条直线的平行线”的双边直尺作图过程.
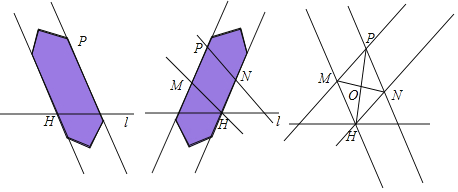
(1)根据小My同学的作图过程,请证明O为PH中点.
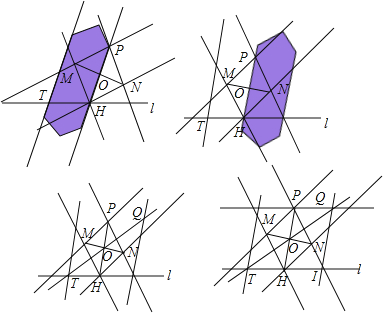
(2)根据小My同学的作图过程,请证明PQ∥l.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据小My同学的作图过程可得,四边形PMHN是平行四边形,根据平行四边形的对角线互相平分,即可得结论;
(2)作OK∥TH交QI于点K,由作图过程可证明△OQK≌△TOH(ASA),可得OQ=OT,进而可以得结论.
解:(1)根据小My同学的作图过程可知:
四边形PMHN是平行四边形,
根据平行四边形的对角线互相平分,
所以O为PH中点.
(2)如图,作OK∥TH交QI于点K,
由作图过程可知:
PH∥QI,
∴OK=HI=TH,
∠QOK=∠OTH,
∠OKQ=∠QIH=∠OHT,
∴△OQK≌△TOH(ASA),
∴OQ=OT,
∵OP=OH,
∴四边形PQHT是平行四边形,
∴PQ∥l.

【题目】常常听说“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形两直角边长a,b与斜边长c之间满足等式:a2+b2=c2”的一个最简单特例.我们把满足a2+b2=c2的三个正整数a,b,c,称为勾股数组,记为(a,b,c).
(1)请在下面的勾股数组表中写出m、n、p合适的数值:
a | b | c | a | b | c |
3 | 4 | 5 | 4 | 3 | 5 |
5 | 12 | m | 6 | 8 | 10 |
7 | 24 | 25 | p | 15 | 17 |
9 | n | 41 | 10 | 24 | 26 |
11 | 60 | 61 | 12 | 35 | 37 |
… | … | … | … | … | … |
平面直角坐标系中,横、纵坐标均为整数的点叫做整点(格点).过x轴上的整点作y轴的平行线,过y轴上的整点作x轴的平行线,组成的图形叫做正方形网格(有时简称网格),这些平行线叫做格边,当一条线段AB的两端点是格边上的点时,称为AB在格边上.顶点均在格点上的多边形叫做格点多边形.在正方形网格中,我们可以利用勾股定理研究关于图形面积、周长的问题,其中利用割补法、作图法求面积非常有趣.
(2)已知△ABC三边长度为4、13、15,请在下面的网格中画出格点△ABC并计算其面积.