题目内容
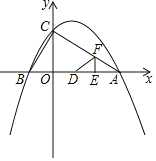
【题目】如图,△ABC为等边三角形,AB=3,若点P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为_____.

【答案】![]()
【解析】
由等边三角形的性质得出∠ABC=∠BAC=60°,AC=AB=3,求出∠APC=120°,当PB⊥AC时,PB长度最小,设垂足为D,此时PA=PC,由等边三角形的性质得出AD=CD=![]() AC=
AC=![]() ,∠PAC=∠ACP=30°,∠ABD=
,∠PAC=∠ACP=30°,∠ABD=![]() ∠ABC=30°,求出PD=AD.tan30°=
∠ABC=30°,求出PD=AD.tan30°=![]() AD=
AD=![]() ,BD=
,BD=![]() AD=
AD=![]() ,即可得出答案.
,即可得出答案.
解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
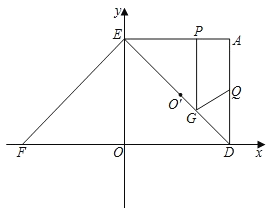
∴点P的运动轨迹是![]() ,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CD=![]() AC=
AC=![]() ,∠PAC=∠ACP=30°,∠ABD=
,∠PAC=∠ACP=30°,∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∴PD=ADtan30°=![]() ×
×![]() =
=![]() ,
,
BD=![]() AD=
AD=![]() ,
,
∴PB=BD﹣PD=![]() ﹣
﹣![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】我们约定:体重在选定标准的![]() %(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
%(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
(1)将这组数据的三个统计量:平均数、中位数和众数填入下表:
平均数 | 中位数 | 众数 |
(2)请你选择其中一个统计量作为选定标准,说明选择的理由.并按此选定标准找出这10名男生中具有“一般体重”的男生.