��Ŀ����
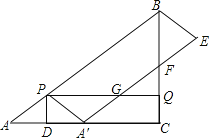
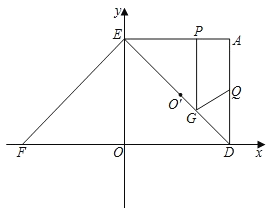
����Ŀ����ͼ������ֱ�ǡ�OEF������ϵ�У���E(0��2)��F(��2��0)����ֱ�ǡ�OEF�Ƶ�E��ʱ����ת90��õ���ADE����A�ڵ�һ�����ڣ�������y=ax2+bx+c������A��E����2a+3b+5=0��
��1���������ߵĽ���ʽ��
��2����ED���е�O'��O'B��OE��B��O'C��OD��C����֤��OBO'CΪ�����Σ�
��3�������P��E��ʼ��EA����ÿ��2�����ٶ����A�ƶ���ͬʱ��Q�ɵ�A��AD����ÿ��1�����ٶ����D�ƶ�������P�ƶ�����Aʱ��P��Q����ͬʱֹͣ���ҹ�P��GP��AE����DE�ڵ�G�����ƶ��Ŀ�ʼ��Ϊt�룮
����S=PQ2(����)����д��S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
����Sȡ��Сʱ�������������Ƿ���ڵ�R��ʹ����P��A��Q��RΪ������ı�����ƽ���ı��Σ�������ڣ����R�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��֤������������3����S=5t2��8t+4(0��t��2)������R������Ϊ��(
����2��֤������������3����S=5t2��8t+4(0��t��2)������R������Ϊ��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
��������
��1��������������ת�����ʵó�A�����꣬�ٸ���E������ó�c��ֵ������һ����⼴�ɣ�
��2������������֤��OBO'CΪ���Σ���������������λ�����ʽ������ó�O'B=OC'���ݴ˽�һ��֤�����ɣ�
��3�����������г���ϵʽ���Ի��ɣ��ڸ��������AP�DZ�ʱ�Լ�PA�ǶԽ���ʱ���������һ���������ۼ��ɣ�
��1����E��F����ֱ�Ϊ��E(0��2)��F(��2��0)��
��OF=OE=2��
������ת���ʿɵã�AE=OE=2��AD=OF=2��
���A������(2��2)��
����E��������������߱���ʽ�������ã� c=2��
�֡�A������Ϊ��(2��2)��
��4a+2b=0��
��2a+3b+5=0��
��������ʽ��������ã�a=![]() ��b=-
��b=-![]() ��
��
�������ߵı���ʽΪ��![]() ��
��
��2����ͼ��ʾ��
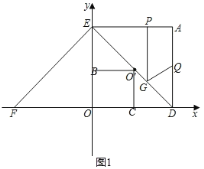
��O'B��OE��O'C��OD����EOD=90������OBO'C����
�֡�O'��ED���е㣬O'B��OE��
��O'B=![]() OD��
OD��
��O'C��OD��
��ͬ���ɵã�O'C=![]() OE��
OE��
��OE=OD��
��O'B=OC'
��OBO'C������
��3���ٵ�P��Q������ֱ�Ϊ��(2t��2)��(2��2��t)��
S=PQ2=(2t��2)2+(t)2=5t2��8t+4(0��t��2)��
��S=5t2��8t+4(0��t��2)��
��5��0����S����Сֵ����ʱt=![]() ��
��
���P��Q������ֱ�Ϊ��(![]() ��2)��(2��
��2)��(2��![]() )������A(2��2)��
)������A(2��2)��
�裺��R(m��n)��n=![]() m2��
m2��![]() m+2��
m+2��
(��)��AP�DZ�ʱ��
��P����ƽ��![]() ����λ�õ�A��
����λ�õ�A��
ͬ����Q(R)����ƽ��![]() ����λ�õ�R(Q)��
����λ�õ�R(Q)��
��2![]() =m����ã�m=
=m����ã�m=![]() ��
��![]() ��
��
�ʵ�R(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
(��)��PA�ǶԽ���ʱ��
���е㹫ʽ�ã�2+![]() =m+2��
=m+2��
��ã�m=![]() ���ʵ�R(
���ʵ�R(![]() ��
��![]() )��
)��
���ϣ���R������Ϊ��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�