题目内容
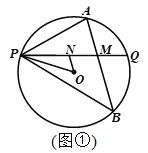
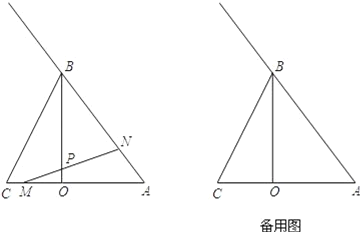
【题目】如图,已知BO是△ABC的AC边上的高,其中BO=8,AO=6,CO=4,点M以2个单位长度/秒的速度自C向A在线段CA上作匀速运动,同时点N以5个单位长度/秒的速度自A向B在射线AB上作匀速运动,MN交OB于点P.当M运动到点A时,点M、N同时停止运动.设点M运动时间为t.
(1)线段AN的取值范围是______.
(2)当0<t<2时,
①求证:MN:NP为定值.
②若△BNP与△MNA相似,求CM的长.
(3)当2<t<5时,若△BNP是等腰三角形,求CM的长.
【答案】(1)0<AN<25;(2)①证明见解析;定值为![]() ;②CM=
;②CM=![]() ;(3)CM=
;(3)CM=![]() .
.
【解析】
(1)首先求出点M运动时间,再求出点N运动的路程即可.
(2)如图1中,①过点N作NH⊥AC于点H,设AN=5k,CM=2k,用含k的代数式表示MH、OH即可解决问题;②只可能是∠MNB=∠MNA=90°,由△MHN∽△MNA∽△BOA,列出比例式即可解决问题.
(3)过点N作NH⊥AC于点H, 设AN=5k,CM=2k,如图2中,当2<t<5时,点M在OA上,由PO∥HN,得![]() ,求出PO=
,求出PO=![]() k,根据BP=BN,列出方程即可解决问题.
k,根据BP=BN,列出方程即可解决问题.
(1)∵AC=OC+AO=10,
点M运动的速度为2单位长度/秒,
∴t=![]() =5,
=5,
∵5×5=25,
∴0<AN<25.
故答案为0<AN<25;
(2)如图1中,当0<t<2时,
①过点N作NH⊥AC于点H,设AN=5k,CM=2k,
∵NH∥BO,
∴![]() ,
,
∴AH=3k,
∴OH=6-3k,OM=4-2k,MH=10-5k,
∵PO∥NH,
∴![]() ;
;
②只可能是∠MNB=∠MNA=90°,
△MHN∽△MNA∽△BOA,
∴![]() ,
,
∴![]() ,
,
∴k=![]() ,
,
∴CM=![]() ;
;
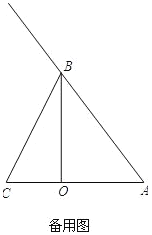
(3)如图2中,当2<t<5时,
过点N作NH⊥AC于点H,设AN=5k,CM=2k,则BN=5k-10,
同(2)可得AH=3k,NH=4k,OH=3k-6,MO=2k-4,
∵PO∥HN,
∴![]() ,
,
∵MH=AH-AM=3k-(10-2k)=5k-10,
∴PO=![]() k,
k,
若BP=BN,则8-![]() k=5k-10,
k=5k-10,
解得:k=![]() ,
,
∴CM=![]() ,
,
若PB=PN或BN=NP,
∵∠PBN>90°,
∴不成立,
∴若△BNP是等腰三角形,CM的长为![]() .
.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案