题目内容
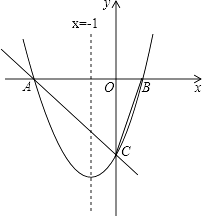
【题目】设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( ) 
A.4
B.5
C.5或3 ![]()
D.4或3 ![]()
【答案】D
【解析】解:由反比例函数的图象得xy=4,当等腰直角△ABC的斜边为底时,该底边上的高为这个底的一半, 即x=2y,2y2=4,
解得:y= ![]() ,
,
则x=2 ![]() ,
,
∴x+y=3 ![]() ;
;
当等腰直角△ABC的一条直角边为底时,该底边上的高为另一条直角边,
即x=y,y2=4,
解得:y=2,
则x=2,
∴x+y=4,
综上知x+y的值为4或3 ![]() .
.
故选:D.
【考点精析】根据题目的已知条件,利用等腰直角三角形和反比例函数的图象的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.

练习册系列答案
相关题目
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
(1)求出下列成绩统计分析表中a,b的值:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.