题目内容
【题目】在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )
A.14.4
B.19.2
C.18.75
D.17
【答案】D
【解析】解:在Rt△ABC中,∠ACB=90°,AC=6,BC=8, ∴AB= ![]() =10,S△ABC=
=10,S△ABC= ![]() ACBC=24.
ACBC=24.
沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,有四种情况:①当AC=AP=6时,如图1所示,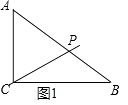
S等腰△ACP= ![]() S△ABC=
S△ABC= ![]() ×24=14.4;②当BC=BP=8时,如图2所示,
×24=14.4;②当BC=BP=8时,如图2所示,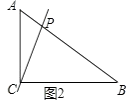
S等腰△BCP= ![]() S△ABC=
S△ABC= ![]() ×24=19.2;③当PA=PB时,如图3所示,
×24=19.2;③当PA=PB时,如图3所示,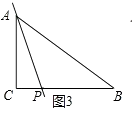
AC2+CP2=PA2 , 即62+(8﹣PB)2=PB2 ,
解得:PB= ![]() ,
,
∴S等腰△PAB= ![]() PBAC=
PBAC= ![]() ×
× ![]() ×6=
×6= ![]() =18.75;④当CA=CP=6时,如图4所示,
=18.75;④当CA=CP=6时,如图4所示,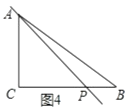
S等腰△CAP= ![]() CACP=
CACP= ![]() ×6×6=18.
×6×6=18.
综上所述:等腰三角形的面积可能为14.4、19.2、18.75或18.
故选D.
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目





