��Ŀ����
����Ŀ��ij��ѧ�㳡���������ͼ1��ʾ����ѧϰ��ֱ���������Ժ���ѧ��ȤС���������˵ij��ȣ���ͼ2����ijһʱ�̣�������ˮƽ��ļн�Ϊ72�㣬���AB��Ӱ��һ��������ƽ̨�ϣ���һ��������б���ϣ��������ƽ̨�ϵ�Ӱ��BCΪ4�ף�����б���ϵ�Ӱ��CDΪ3�ף�AB��BC��ͬһʱ�̣���1���������PQ��б���ϵ�Ӱ��QRΪ2�ף������AB�ij��ȣ��������ȷ��0.1�ף��ο����ݣ�sin72���0.95��cos72���0.31��tan72���3.08����
���𰸡��⣺��ͼ����CM��AB��AD�ڵ�M��MN��AB�ڵ�N��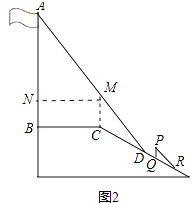
������ ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��CM=���ף���
��Rt��AMN�У��ߡ�ANM=90�㣬MN=BC=4�ף���AMN=72�㣬
��tan 72��= ![]() ��
��
��AN=MNtan 72���4��3.08��12.3���ף���
��MN��BC��AB��CM��
���ı���MNBC��ƽ���ı��Σ�
��BN=CM=�ף�
��AB=AN+BN=13.8�ף�
����������ͼ��CM��AB��AD��M��MN��AB��N������ ![]() =
= ![]() �����CM����RT��AMN������tan72��=
�����CM����RT��AMN������tan72��= ![]() �����AN���ɽ�����⣮
�����AN���ɽ�����⣮

��ϰ��ϵ�д�
 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
�����Ŀ