题目内容
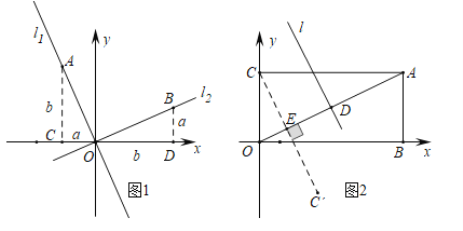
【题目】如图,平面直角坐标系中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图象为
的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
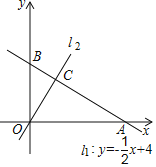
【答案】(1)m=2;![]() 的解析式为:
的解析式为:![]() ;(2)8;(3)k的值为
;(2)8;(3)k的值为![]() 或
或![]() 或1
或1
【解析】
(1)将点C坐标代入![]() 即可求出m的值,利用待定系数法即可求出l2的解析式;
即可求出m的值,利用待定系数法即可求出l2的解析式;
(2)根据一次函数![]() ,可求出A(8,0),B(0,4),结合点C的坐标,利用三角形面积的计算公式即可求出
,可求出A(8,0),B(0,4),结合点C的坐标,利用三角形面积的计算公式即可求出![]() 的值;
的值;
(3)若![]() ,
,![]() ,
,![]() 不能围成三角形,则有三种情况,①当l1∥l3时;②当l2∥l3时;③当l3过点C时,根据得出k的值即可.
不能围成三角形,则有三种情况,①当l1∥l3时;②当l2∥l3时;③当l3过点C时,根据得出k的值即可.
解:(1)将点![]() 代入
代入![]() 得
得![]() ,解得m=2,
,解得m=2,
∴C(2,3)
设l2的解析式为y=nx,
将点C代入得:3=2n,
∴![]() ,
,
∴![]() 的解析式为:
的解析式为:![]() ;
;
(2)如图,过点C作CE⊥y轴于点E,作CF⊥x轴于点F,
∵C(2,3)
∴CE=2,CF=3,
∵一次函数![]() 的图象
的图象![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,
∴当x=0时,y=4,当y=0时,x=8,
∴A(8,0),B(0,4),
∴OA=8,OB=4,
∴![]()
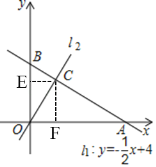
(3)①当l1∥l3时,![]() ,
,![]() ,
,![]() 不能围成三角形,此时k=
不能围成三角形,此时k=![]() ;
;
②当l2∥l3时,![]() ,
,![]() ,
,![]() 不能围成三角形,此时k=
不能围成三角形,此时k=![]() ;
;
③当l3过点C时,将点C代入![]() 中得:
中得:![]() ,解得k=1,
,解得k=1,
综上所述,k的值为![]() 或
或![]() 或1.
或1.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目