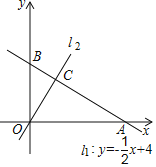Question

【题目】阅读下列两段材料，回答问题：

材料一：点，的中点坐标为．例如，点，的中点坐标为，即

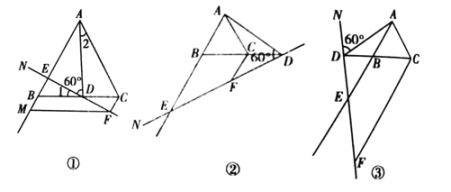
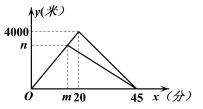
材料二：如图1，正比例函数和的图象相互垂直，分别在和上取点、使得分别过点作轴的垂线，垂足分别为点．显然，，设，，则，．．于是，所以的值为一个常数，一般地，一次函数，可分别由正比例函数平移得到.

所以，我们经过探索得到的结论是：任意两个一次函数，的图象相互垂直，则的值为一个常数.

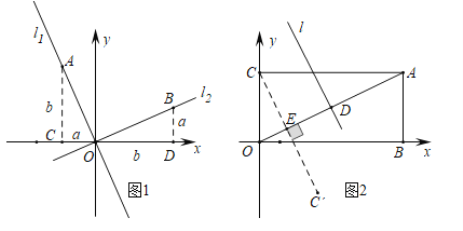
（1）在材料二中，=______（写出这个常数具体的值）

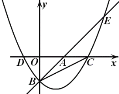
（2）如图2，在矩形中，点是中点，用两段材料的结论，求点的坐标和的垂直平分线的解析式;

（3）若点与点关于对称，用两段材料的结论，求点的坐标.

Answer 1

【答案】(1)-1；(2) ， ；（3）

【解析】

（1）将k1，k2的值相乘，即可得出结论；
（2）由点O，A的坐标可求出其中点D的坐标，由点A的坐标可得出直线OA的解析式，由（1）的结论可设直线l的解析式为y=-2x+m，代入点D的坐标即可求出直线l的解析式；
（3）由矩形的性质可得出点C的坐标，由（1）的结论可设直线CC′的解析式为y=-2x+n，代入点C的坐标可求出直线CC′的解析式，联立直线CC′和OA的解析式成方程组，通过解方程组可求出点E的坐标，再由点E为线段CC′的中点可求出点C′的坐标．

（1）∵=-,=,

∴k1k2=-=-1.

故答案为-1.

（2）∵点O的坐标为（0，0），点A的坐标为（4，2），点D是OA中点，
∴点D的坐标为（2，1）．
∵点A的坐标为（4，2），
∴直线OA的解析式为y=x．
∵直线l⊥直线OA，
∴设直线l的解析式为y=-2x+m．
∵直线l过点D（2，1），
∴1=-4+m，解得：m=5，
∴OA的垂直平分线的解析式为y=-2x+5．

（3）∵点A的坐标为（4，2），四边形OBAC为矩形，
∴点C的坐标为（0，2）．
设直线CC′的解析式为y=-2x+n，
∵直线CC′过点C（0，2），
∴n=2，即直线CC′的解析式为y=-2x+2．
联立直线CC′和OA的解析式成方程组，得：，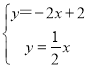

解得：

∴点E的坐标为（ ）

∵点E为线段CC′的中点，
∴点C′的坐标为（ ），即（-）.

故答案为(1)-1；(2) ， ；（3）