题目内容
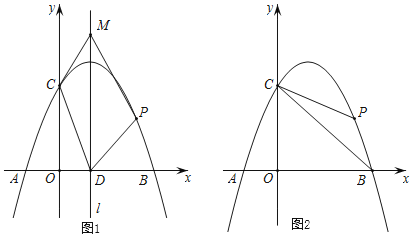
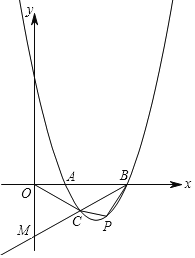
【题目】如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)OC=![]() ;(2)y=
;(2)y=![]() x﹣
x﹣![]() ,抛物线解析式为y=
,抛物线解析式为y=![]() x2﹣
x2﹣![]() x+2
x+2![]() ;(3)点P存在,坐标为(
;(3)点P存在,坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)令y=0,求出x的值,确定出A与B坐标,根据已知相似三角形得比例,求出OC的长即可;
(2)根据C为BM的中点,利用直角三角形斜边上的中线等于斜边的一半得到OC=BC,确定出C的坐标,利用待定系数法确定出直线BC解析式,把C坐标代入抛物线求出a的值,确定出二次函数解析式即可;
(3)过P作x轴的垂线,交BM于点Q,设出P与Q的横坐标为x,分别代入抛物线与直线解析式,表示出坐标轴,相减表示出PQ,四边形ACPB面积最大即为三角形BCP面积最大,三角形BCP面积等于PQ与B和C横坐标之差乘积的一半,构造为二次函数,利用二次函数性质求出此时P的坐标即可.
(1)由题可知当y=0时,a(x﹣1)(x﹣3)=0,
解得:x1=1,x2=3,即A(1,0),B(3,0),
∴OA=1,OB=3
∵△OCA∽△OBC,
∴OC:OB=OA:OC,
∴OC2=OAOB=3,
则OC=![]() ;
;
(2)∵C是BM的中点,即OC为斜边BM的中线,
∴OC=BC,
∴点C的横坐标为![]() ,
,
又OC=![]() ,点C在x轴下方,
,点C在x轴下方,
∴C(![]() ,﹣
,﹣![]() ),
),
设直线BM的解析式为y=kx+b,
把点B(3,0),C(![]() ,﹣
,﹣![]() )代入得:
)代入得: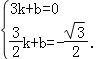 ,
,
解得:b=﹣![]() ,k=
,k=![]() ,
,
∴y=![]() x﹣
x﹣,
又∵点C(![]() ,﹣
,﹣![]() )在抛物线上,代入抛物线解析式,
)在抛物线上,代入抛物线解析式,
解得:a=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x+2
x+2![]() ;
;
(3)点P存在,
设点P坐标为(x,![]() x2﹣
x2﹣![]() x+2
x+2![]() ),过点P作PQ⊥x轴交直线BM于点Q,
),过点P作PQ⊥x轴交直线BM于点Q,
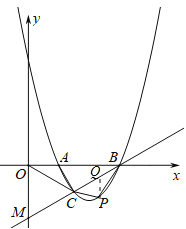
则Q(x,![]() x﹣
x﹣![]() ),
),
∴PQ=![]() x﹣
x﹣![]() ﹣(
﹣(![]() x2﹣
x2﹣![]() x+2
x+2![]() )=﹣
)=﹣![]() x2+3
x2+3![]() x﹣3
x﹣3![]() ,
,
当△BCP面积最大时,四边形ABPC的面积最大,
S△BCP=![]() PQ(3﹣x)+
PQ(3﹣x)+![]() PQ(x﹣
PQ(x﹣![]() )=
)=![]() PQ=﹣
PQ=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ,
,
当x=﹣![]() 时,S△BCP有最大值,四边形ABPC的面积最大,此时点P的坐标为(
时,S△BCP有最大值,四边形ABPC的面积最大,此时点P的坐标为(![]() ,﹣
,﹣![]() ).
).

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案