题目内容
【题目】如图,点C为线段AB上一点,△DAC、△ECB都是等边三角形,AE、DC交于点M,DB、EC交于点N,DB、AE交于点P,连接MN,下列说法中正确的个数有( )

①MN∥AB;②∠DPM=60°;③∠DAP=∠PEC;④△ACM≌△DCN;⑤若∠DBC=30°,则∠AEB=80°
A.2个B.3个C.4个D.5个
【答案】C
【解析】
根据题目中的信息和等边三角形的性质,再应用三角形全等的方法逐个判断即可.
∵△DAC、△ECB都是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ADC=∠DCE=60°,
∴AD∥CE,∴∠DAP=∠PEC,故③正确;
在△ACE与△BCD中,
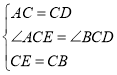
∴△ACE≌△BCD,∴∠CAE=∠CDB,
∵∠PMD=∠AMC,∴∠DPM=∠ACM=60°,故②正确,
在△ACM与△DCN中,
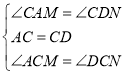
∴△ACM≌△DCN,故④正确;
∴CM=CN,∴△CMN是等边三角形,
∴∠CMN=60°,∴∠CMN=∠ACD,∴MN∥AB,故①正确;
∵∠DBC=30°,∴∠PBE=30°,
∵∠DPM=60°,∴∠BPE=60°,∴∠AEB=90°.故⑤错误;
正确的个数为4个,故选C.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目