题目内容
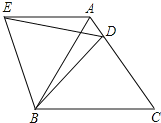
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据已知可得到∠A=∠B=90°,DE=CE,AD=BE从而利用HL判定两三角形全等;
(2)由三角形全等可得到对应角相等,对应边相等,由已知可推出∠DEC=90°,由已知我们可求得BE、AE的长,再利用勾股定理求得ED、DC的长.
(1)∵AD∥BC,∠A=90°,∠1=∠2,
∴∠A=∠B=90°,DE=CE.
∵AD=BE,
∴△ADE≌△BEC.
(2)由△ADE≌△BEC得∠AED=∠BCE,AD=BE.
∴∠AED+∠BEC=∠BCE+∠BEC=90°.
∴∠DEC=90°.
又∵AD=6,AB=14,
∴BE=AD=6,AE=14-6=8.
∵∠1=∠2,
∴ED=EC=![]() .
.
∴DC=![]() .
.

练习册系列答案
相关题目
【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量 | 年用水量 (立方米) | 水价 (元/立方米) |
第一阶梯 | 0~180(含) | 5.00 |
第二阶梯 | 181~260(含) | 7.00 |
第三阶梯 | 260以上 | 9.00 |
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?