��Ŀ����
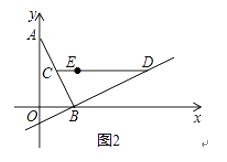
����Ŀ����ͼ���ڱ߳�Ϊ10������ABCD�У��Խ���BD��16���Խ���AC��BD�ཻ�ڵ�G����O��ֱ��BD�ϵĶ��㣬OE��AB��E��OF��AD��F.
(1)��Խ���AC�ij�������ABCD�������
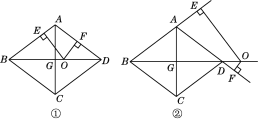
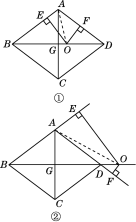
(2)��ͼ�٣�����O�ڶԽ���BD���˶�ʱ��OE��OF��ֵ�Ƿ����仯����˵�����ɣ�
(3)��ͼ�ڣ�����O�ڶԽ���BD���ӳ�����ʱ��OE��OF��ֵ�Ƿ����仯�������䣬��˵�����ɣ����仯����̽��OE��OF֮���������ϵ��
���𰸡���1��12��96 ��2���𰸼����� ��3���𰸼�����
��������
��1���������εĶԽ����ഹֱƽ�����BG�������ù��ɶ�����ʽ���AG��Ȼ�����AC=2AG���㼴�ɵý⣻�ٸ������ε�������ڶԽ��߳˻���һ����ʽ���㼴�ɵý⣻
��2������AO������S��ABD=S��ABO+S��ADO��ʽ���㼴�ɵý⣻
��3������AO������S��ABD=S��ABO-S��ADO��ʽ�������ɵý�.
�⣺(1)������ABCD�У�AG��CG��AC��BD��BG��![]() BD��
BD��![]() ��16��8��
��16��8��
�ɹ��ɶ�����AG��![]() ��
��
����AC��2AG��2��6��12.
��������ABCD�������![]() AC��BD��
AC��BD��![]() ��12��16��96.
��12��16��96.
(2)�������仯���������£���ͼ�٣�����AO����S��ABD��S��ABO��S��AOD��
����![]() BD��AG��
BD��AG��![]() AB��OE��
AB��OE��![]() AD��OF��
AD��OF��
��![]() ��16��6��
��16��6��![]() ��10��OE��
��10��OE��![]() ��10��OF.
��10��OF.
���OE��OF��9.6���Ƕ�ֵ�����䣮
(3)�����仯����ͼ�ڣ�����AO����S��ABD��S��ABO��S��AOD��
����![]() BD��AG��
BD��AG��![]() AB��OE��
AB��OE��![]() AD��OF.
AD��OF.
��![]() ��16��6��
��16��6��![]() ��10��OE��
��10��OE��![]() ��10��OF.
��10��OF.
���OE��OF��9.6���Ƕ�ֵ�����䣮
����OE��OF��ֵ�����仯��OE��OF֮���������ϵΪOE��OF��9.6.

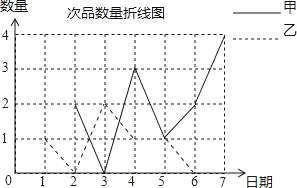
����Ŀ���ס�����������ͬʱ�ӹ�ͬһ��������ָ�������7���Ʒ��ÿ����ֵĴ�Ʒ��������Ƴ����²�������ͳ��ͼ�ͱ�������ͼ������Ϣ������������⣺
���ͳ��������
���� �� | ���� | ��λ�� | ƽ���� | ���� |
�� | �� �� | �� �� | 2 |
|
�� | 1 | 1 | 1 |
|
��Ʒ����ͳ�Ʊ���
���� �� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�� | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
�� | 1 | 0 | 2 | 1 | 1 | 0 | �� �� |
��1����ȫͼ������
��2���ж�˭���ִ�Ʒ�IJ���С��
��3�������Ҽӹ��������30����ִ�Ʒ���ټ���