Question

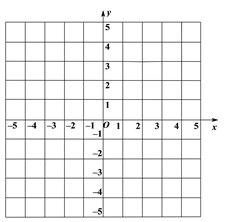
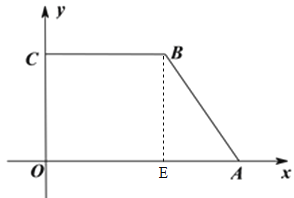
【题目】如图，在平面直角坐标系中，点A、C分别在x轴上、y轴上，CB//OA，OA=8，若点B的坐标为(a,b)，且b=.

（1）直接写出点A、B、C的坐标；

（2）若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动，当直线PC把四边形OABC分成面积相等的两部分停止运动，求P点运动时间；

（3）在（2）的条件下，在y轴上是否存在一点Q，连接PQ，使三角形CPQ的面积与四边形OABC的面积相等？若存在，求点Q的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）A（8,0），B（4,4），C（0.4）；（2）t=；（3）（0,13），（0，－5）

【解析】分析：（1）根据线段的长和线段的特点以及二次根式有意义的条件确定出点的坐标；

（2）先求出S四边形OABC=24，从而得到×OP×4=12，求出OP即可得到结论；

（3）根据四边形OABC的面积求出△CPQ的面积是24，即可求出点Q的坐标．

详解：（1）过B作BE⊥OA于E．∵a-4≥0且4-a≥0，∴a=4，∴b=4，∴B（4，4），∴OC=EB=4，∴C（0.4）．∵OA=8，∴A（8，0）；

（2）设运动时间t秒，∴OP=2t， ∴2t4=，∴t=3．

（3）设Q（0，y）， ∵，∴ =(4+8)4，

∴=13，=－5，∴（0，13），（0，－5）