Question

【题目】某森林公园从正门到侧门有一条公路供游客运动，甲徒步从正门出发匀速走向侧门，出发一段时间开始休息，休息了0.6小时后仍按原速继续行走．乙与甲同时出发，骑自行车从侧门匀速前往正门，到达正门后休息0.2小时，然后按原路原速匀速返回侧门．图中折线分别表示甲、乙到侧门的路程y（km）与甲出发时间x（h）之间的函数关系图象．根据图象信息解答下列问题．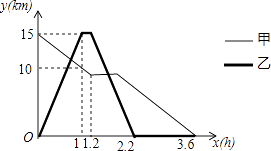

（1）求甲在休息前到侧门的路程y（km）与出发时间x（h）之间的函数关系式．
（2）求甲、乙第一次相遇的时间．
（3）直接写出乙回到侧门时，甲到侧门的路程．

Answer 1

【答案】
（1）解：设甲在休息前到侧门的路程y（km）与出发时间x（h）之间的函数关系式为：y=kx+b，

∵点（0，15）和点（1，10）在此函数的图象上，

∴ ，

解得k=﹣5，b=15．

∴y=﹣5x+15．

即甲在休息前到侧门的路程y（km）与出发时间x（h）之间的函数关系式为：y=﹣5x+15

（2）解：设乙骑自行车从侧门匀速前往正门对应的函数关系式y=kx，

将（1，15）代入可得k=15，

∴乙骑自行车从侧门匀速前往正门对应的函数关系式y=15x，

∴

解得x=0.75．

即第一次相遇时间为0.75h

（3）解：乙回到侧门时，甲到侧门的路程是7km．

设甲休息了0.6小时后仍按原速继续行走对应的函数解析式为：y=kx+b．

将x=1.2代入y=﹣5x+15得，y=9．

∵点（1.8，9），（3.6，0）在y=kx+b上，

∴ ，

解得k=﹣5，b=18．

∴y=﹣5x+18．

将x=2.2代入y=﹣5x+18，得y=7．

即乙回到侧门时，甲到侧门的路程是7km

【解析】（1）先依据函数图象确定出函数图象经过的点的坐标，然后再利用待定系数法求解即可；
（2）根据函数图象可以分别求得甲乙刚开始两端对应的函数解析式，然后将两函数解析式联立组成方程组，通过解方程组可求得第一次相遇的时间；
（3）根据函数图象可以得到在最后一段甲对应的函数解析式，乙到侧门时时间为2.2h，从而可以得到乙回到侧门时，甲到侧门的路程．