题目内容
【题目】已知:如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 在射线
在射线![]() 上,以
上,以![]() 为半径的
为半径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
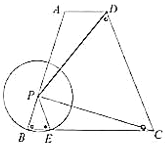
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)联结![]() ,当
,当![]() 时,以
时,以![]() 为圆心半径为
为圆心半径为![]() 的
的![]() 与
与![]() 相交,求
相交,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
![]() 根据梯形的性质得到
根据梯形的性质得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,根据平行线的判定定理即可得到结论;
,根据平行线的判定定理即可得到结论;
![]() 分别过P、A、D作BC的垂线,垂足分别为点H、F、
分别过P、A、D作BC的垂线,垂足分别为点H、F、![]() 推出四边形ADGF是矩形,
推出四边形ADGF是矩形,![]() ,求得
,求得![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到![]() ,
,![]() ,求得
,求得![]() ,根据勾股定理即可得到结论;
,根据勾股定理即可得到结论;
![]() 作
作![]() 交DC于
交DC于![]() 推出四边形PDME是平行四边形
推出四边形PDME是平行四边形![]() 得到
得到![]() ,即
,即![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,根据相切两圆的性质即可得到结论.
,根据相切两圆的性质即可得到结论.
![]() 证明:梯形ABCD,
证明:梯形ABCD,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 解:分别过P、A、D作BC的垂线,垂足分别为点H、F、G.
解:分别过P、A、D作BC的垂线,垂足分别为点H、F、G.
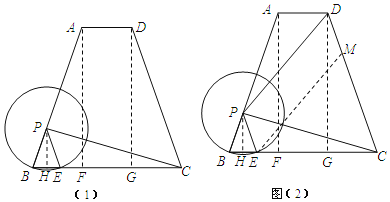
![]() 梯形ABCD中,
梯形ABCD中,![]() ,
,
,![]() ,
,![]() ,
,
![]() 四边形ADGF是矩形,
四边形ADGF是矩形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,即
,即![]() ,
,
![]() 解:作
解:作![]() 交DC于M.
交DC于M.
![]() ,
,
![]() 四边形PDME是平行四边形.
四边形PDME是平行四边形.
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() .
.
![]() ∽
∽![]() ,
,
![]() ,即
,即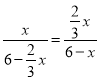 ,
,
解得:![]() ,
,
即![]() ,
,
![]() ,
,
当两圆外切时,![]() ,即
,即![]() 舍去
舍去![]() ;
;
当两圆内切时,![]() ,即
,即![]() 舍去
舍去![]() ,
,![]() ;
;
即两圆相交时,![]() .
.

练习册系列答案
相关题目
【题目】小明和小丽暑期参加工厂社会实践活动,师傅将他们工作第一周每天生产的合格产品的个数整理成如表两组数据,那么关于他们工作第一周每天生产的合格产品个数,下列说法中正确的是( )
小明 | 2 | 6 | 7 | 7 | 8 |
小丽 | 2 | 3 | 4 | 8 | 8 |
A. 小明的平均数小于小丽的平均数
B. 两人的中位数相同
C. 两人的众数相同
D. 小明的方差小于小丽的方差