题目内容
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在
在![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() .
.
①如图![]() ,当点
,当点![]() 运动到某位置时,以
运动到某位置时,以![]() ,
,![]() 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点![]() 的坐标;
的坐标;
②如图![]() ,过点
,过点![]() ,
,![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() ;(2)①
;(2)①![]() 点的坐标是
点的坐标是![]() ;②
;②![]() .
.
【解析】
(1)由直线的解析式y=x+4易求点A和点C的坐标,把A和C的坐标分别代入y=-![]() x2+bx+c求出b和c的值即可得到抛物线的解析式;
x2+bx+c求出b和c的值即可得到抛物线的解析式;
(2)①若以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,则PQ∥AO,再根据抛物线的对称轴可求出点P的横坐标,由(1)中的抛物线解析式,进而可求出其纵坐标,问题得解;
②过P点作PF∥OC交AC于点F,因为PF∥OC,所以△PEF∽△OEC,由相似三角形的性质:对应边的比值相等可求出PF的长,进而可设点点F(x,x+4),利用(![]() x2x+4)(x+4)=
x2x+4)(x+4)=![]() ,可求出x的值,解方程求出x的值可得点P的坐标,代入直线y=kx即可求出k的值.
,可求出x的值,解方程求出x的值可得点P的坐标,代入直线y=kx即可求出k的值.
解:![]() ∵直线
∵直线![]() 经过
经过![]() ,
,![]() 两点,
两点,
∴![]() 点坐标是
点坐标是![]() ,点
,点![]() 坐标是
坐标是![]() ,
,
又∵抛物线过![]() ,
,![]() 两点,
两点,
∴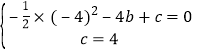 ,解得:
,解得:![]() ,
,
∴抛物线的解析式为![]() .
.
![]() ①如图
①如图![]()
∵![]() ,
,
∴抛物线的对称轴是直线![]() .
.
∵以![]() ,
,![]() 为邻边的平行四边形的第四个顶点
为邻边的平行四边形的第四个顶点![]() 恰好也在抛物线上,
恰好也在抛物线上,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() 都在抛物线上,
都在抛物线上,
∴![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 点的横坐标是
点的横坐标是![]() ,
,
∴当![]() 时,
时,![]() ,
,

∴![]() 点的坐标是
点的坐标是![]() ;
;
②过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
设点![]() ,
,
∴![]() ,
,
化简得:![]() ,解得:
,解得:![]() ,
,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 点坐标是
点坐标是![]() 或
或![]() .
.
又∵点![]() 在直线
在直线![]() 上,
上,
∴![]() .
.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】![]() 在方格中的位置如图所示.
在方格中的位置如图所示.
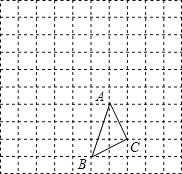
(1)请在方格纸上(小方格的边长为1)建立平面直角坐标系,使得A、B两点的坐标分别为![]() ,
,![]() .并求出C点的坐标;
.并求出C点的坐标;
(2)作出![]() 关于x轴对称的
关于x轴对称的![]() ,并写出
,并写出![]() 、
、![]() 两点的坐标.
两点的坐标.
(3)求![]() 的面积。
的面积。
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
![]() 根据上表填空:
根据上表填空:
①抛物线与![]() 轴的交点坐标是________和________;
轴的交点坐标是________和________;
②抛物线经过点![]() ,________
,________![]() ;
;
③在对称轴右侧,![]() 随
随![]() 增大而________;
增大而________;
![]() 试确定抛物线
试确定抛物线![]() 的解析式.
的解析式.


