题目内容
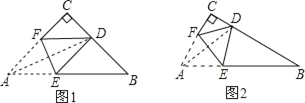
【题目】直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、F.
(1)如果∠AFE=65°,求∠CDF的度数;
(2)若折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.

【答案】(1)40°;(2)45°或30°,图见解析.
【解析】
(1)根据翻折的性质,得到∠AFE=∠DFE=65°,即可求出∠CFD=180°﹣65°﹣65°=50°,根据直角三角形两个锐角互余的性质即可求出∠CDF的度数.
(2)先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
(1)根据翻折不变性可知:∠AFE=∠DFE=65°,
∴∠CFD=180°﹣65°﹣65°=50°,
∵∠C=90°,
∴∠CDF=90°﹣50°=40°.
(2)∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD, AE=DE,
∴∠FDA=![]() ∠CFD=22.5°,∠DEB=2x°,
∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.此时∠B=2x=45°;
见图形(1),说明:图中AD应平分∠CAB.
②当BD=BE时,则∠B=(180°﹣4x)°,
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,此时∠B=(180﹣4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则![]()
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+![]() ,
,
此方程无解.
∴DE=BE不成立.
综上所述:∠B=45°或30°.