题目内容
如图，在△ABC中，∠ACB＝90º，∠A＝30º，BC＝1．过点C作CC1⊥AB于C1，
过点C1作C1C2⊥AC于C2，过点C2作C2C3⊥AB于C3，…，按此作发进行下去，则can
＝ ．
过点C1作C1C2⊥AC于C2，过点C2作C2C3⊥AB于C3，…，按此作发进行下去，则can
＝ ．
分析：通过题意可以计算出AB="2" AC=
，根据题意特殊角的三角函数值即可推出
=
，可得AC1=
= 
，同理即可推出AC2= 
，AC3=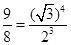
，所以ACn=
．
解答：解：∵∠ACB=90°，∠A=30°，BC=1，
∴AB="2" AC=，
∵CC1⊥AB于C1，=，
∴AC1==，
∵C1C2⊥AC，C2C3⊥AB，
∴同理，AC2=，AC3=，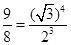
∴ACn=．
故答案为．
，根据题意特殊角的三角函数值即可推出=，可得AC1== ，同理即可推出AC2= ，AC3=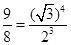，所以ACn=．解答：解：∵∠ACB=90°，∠A=30°，BC=1，
∴AB="2" AC=
，∵CC1⊥AB于C1，
=，∴AC1=
=，∵C1C2⊥AC，C2C3⊥AB，
∴同理，AC2=
，AC3=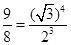，∴ACn=
．故答案为
．
练习册系列答案
全优点练单元计划系列答案
相关题目
中，∠F="90°，点B、C分别在AD、FD上，以AB为直径的半圆O" 过点C，
，
且点E恰好落在直径AB上.
_____
__；并证明你的结论.
，
，从B点测得D点的仰角
为60°，从A点测得D点
为30°，已知甲建筑物高AB=36米．
）
塔的高度，小莹利用自制的测角仪，
在C
或
