题目内容
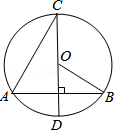
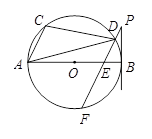
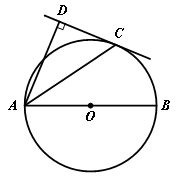
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=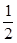 ,求AC的长.
,求AC的长.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=
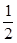 ,求AC的长.
,求AC的长.
(1)PF∥AC;理由见解析;(2)2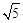 .
.
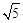 .
.试题分析:(1)连接BC,根据三角形内角和定理求出∠CAB=∠PEB,根据平行线的判定推出即可.
(2)求出sin∠ABC=sin∠P=
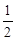 ,代入求出即可.
,代入求出即可.(1)解:直线BP和⊙O相切,
理由:连接BC,
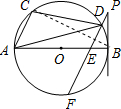
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵直线BP和⊙O相切,
∴∠PBA=90°,
∴∠P+∠PEB=90°,
∵∠P=∠ADC,
∴∠PEB=∠CAB,
∴PF∥AC;
(2)解:由已知,得∠ACB=90°,∠P=∠ADC=∠ABC,⊙O的半径为5,
∴AB=10,
∵tan∠P=
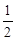 ,
,∴sin∠ABC=
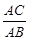 ,
,∴AC=AB×
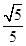 =2
=2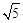 .
.
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
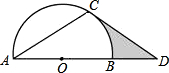
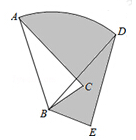
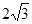 ,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .
,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .