Question

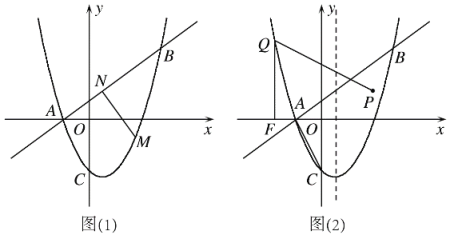
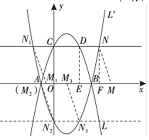
【题目】如图，抛物线交轴于，交轴于，直线平行于轴，与抛物线另一个交点为．

（1）求抛物线的函数表达式及点D的坐标；

（2）若抛物线与抛物线关于轴对称，是轴上的动点，在抛物线上是否存在一点，使得以为顶点且为边的四边形是平行四边形，若存在，请求出点的坐标，若不存在，请说明理由.

Answer 1

【答案】（1）；（2，3）（2）存在；(或(或或

【解析】

（1）利用点A，B的坐标设抛物线的交点式解析式，再将点C代入即可求解，再令，即可求出D点坐标；

（2）先求出抛物线的解析式，再过点作轴于点，过点作轴于点，根据平行四边形的性质可得，进而证明得到，故可求出N点坐标．

解：(1)令，则，∴．

设抛物线的函数表达式，

将点代人，

得，，

解得，，

∴抛物线的函数表达式为．

令，即，解得

．

(2)∵抛物线与抛物线关于轴对称，

又，

∴抛物线的函数表达式为．

过点作轴于点，过点作轴于点，

当以为顶点且为边的四边形是平行四边形时，，

∴∠DBE=∠NMF，

又∠DEB=∠NFM=90°

∴

，即．

①当时，

解得，

∴，

②当时，

解得，

∴．

综上，满足条件的点的坐标为(或(或或．