题目内容
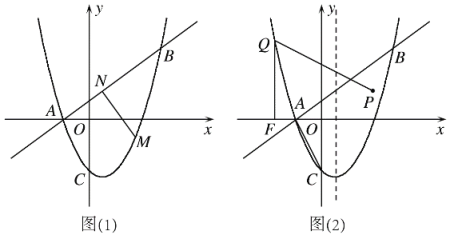
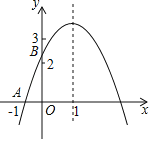
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:
①当﹣1<x<3时,y>0;②﹣1<a<﹣![]() ;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
【答案】①②③
【解析】
①先由抛物线的对称性求得抛物线与x轴令一个交点的坐标为(3,0),从而可知当当﹣1<x<3时,y>0;②设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a.由抛物线与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),可知2<﹣3a<3;③由二次函数的最大值是y=a+b+c,从而可知a+b+c>am2+bm+c(m≠1),④由![]() >2,a<0,从而求得4ac﹣b2<8a.
>2,a<0,从而求得4ac﹣b2<8a.
解:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当﹣1<x<3时,y>0,故①正确;
②设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,
令x=0得:y=﹣3a.
∵抛物线与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),
∴2<﹣3a<3.
解得:﹣1<a<﹣![]() ,故②正确;
,故②正确;
③∵当x=1时,函数有最大值,即a+b+c>am2+bm+c(m≠1),
∴a+b>m(am+b),故③正确;
④∵![]() >2,a<0,
>2,a<0,
∴4ac﹣b2<8a,故④错误,
故答案为①②③.

 天天向上口算本系列答案
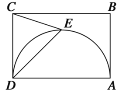
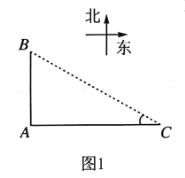
天天向上口算本系列答案【题目】如图1,![]() 是聊城市开发区三个垃圾存放点,点
是聊城市开发区三个垃圾存放点,点![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向, ![]() 米.八位环卫工人分别测得的
米.八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
|
|
|
|
|
|
|
|
|
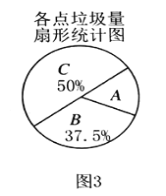
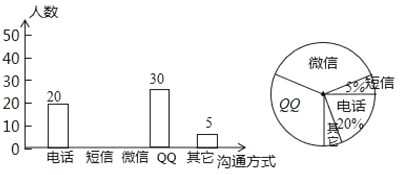
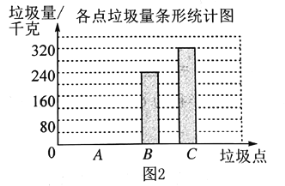
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2、图3.
![]() 求表中
求表中![]() 长度的平均数
长度的平均数![]() ;
;
![]() 求
求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
![]() 用(1)中的
用(1)中的![]() 作为
作为![]() 的长度,要将
的长度,要将![]() 处的垃圾沿道路
处的垃圾沿道路![]() 都运到
都运到![]() 处,已知运送
处,已知运送![]() 千克垃圾每米的费用为
千克垃圾每米的费用为![]() 元,求运垃圾所需的费用(结果保留根号).
元,求运垃圾所需的费用(结果保留根号).