题目内容
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
【答案】(1)制作一件![]() 获利15元,制作一件
获利15元,制作一件![]() 获利120元(2)
获利120元(2)![]() (3)此时制作
(3)此时制作![]() 产品的13人,
产品的13人,![]() 产品的26人,
产品的26人,![]() 产品的26人,获利最大,最大利润为2198元
产品的26人,获利最大,最大利润为2198元
【解析】
(1)设制作一件![]() 获利
获利![]() 元,则制作一件
元,则制作一件![]() 获利(
获利(![]() )元,由题意得:
)元,由题意得:![]() ;(2)设每天安排
;(2)设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,则
,则![]() 人制作
人制作![]() ,于是有:
,于是有:![]() ;(3)列出二次函数,
;(3)列出二次函数,![]() ,再求函数最值即可.
,再求函数最值即可.
(1)设制作一件![]() 获利
获利![]() 元,则制作一件
元,则制作一件![]() 获利(
获利(![]() )元,由题意得:
)元,由题意得:
![]() ,解得:
,解得:![]() ,
,
经检验,![]() 是原方程的根,
是原方程的根,
当![]() 时,
时,![]() ,
,
答:制作一件![]() 获利15元,制作一件
获利15元,制作一件![]() 获利120元.
获利120元.
(2)设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,则
,则![]() 人制作
人制作![]() ,于是有:
,于是有:
![]() ,
,
∴![]()
答:![]() 与
与![]() 之间的函数关系式为∴
之间的函数关系式为∴![]() .
.
(3)由题意得:
![]() ,
,
又∵![]()
∴![]() ,
,
∵![]() ,对称轴为
,对称轴为![]() ,而
,而![]() 时,
时,![]() 的值不是整数,
的值不是整数,
根据抛物线的对称性可得:
当![]() 时,
时,![]() 元.
元.
此时制作![]() 产品的13人,
产品的13人,![]() 产品的26人,
产品的26人,![]() 产品的26人,获利最大,最大利润为2198元.
产品的26人,获利最大,最大利润为2198元.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
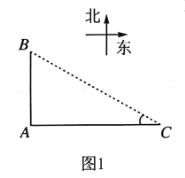
三新快车金牌周周练系列答案【题目】如图1,![]() 是聊城市开发区三个垃圾存放点,点
是聊城市开发区三个垃圾存放点,点![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向, ![]() 米.八位环卫工人分别测得的
米.八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
|
|
|
|
|
|
|
|
|
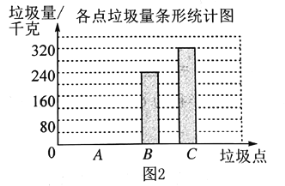
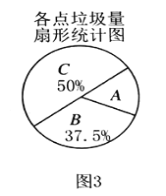
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2、图3.
![]() 求表中
求表中![]() 长度的平均数
长度的平均数![]() ;
;
![]() 求
求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
![]() 用(1)中的
用(1)中的![]() 作为
作为![]() 的长度,要将
的长度,要将![]() 处的垃圾沿道路
处的垃圾沿道路![]() 都运到
都运到![]() 处,已知运送
处,已知运送![]() 千克垃圾每米的费用为
千克垃圾每米的费用为![]() 元,求运垃圾所需的费用(结果保留根号).
元,求运垃圾所需的费用(结果保留根号).
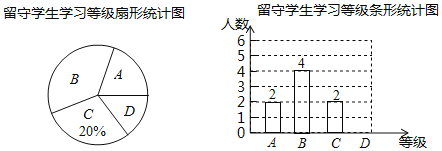
【题目】垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某班举行了专题活动,对200件垃圾进行分类整理,得到下列统计图表,请根据统计图表回答问题:(其中A:可回收垃圾;B:厨余垃圾;C:有害垃圾;D:其它垃圾).
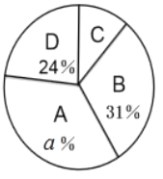
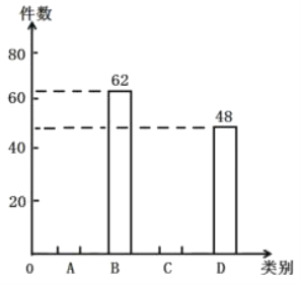
类别 | 件数 |
A | 70 |
B | b |
C | c |
D | 48 |
(1)![]() ________;
________;![]() ________;
________;
(2)补全图中的条形统计图;
(3)有害垃圾C在扇形统计图中所占的圆心角为多少?