题目内容
【题目】等边三角形ABC的边长为4 cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以每秒![]() cm的速度同时开始运动,运动过程中DE与BC相交于点P.
cm的速度同时开始运动,运动过程中DE与BC相交于点P.

(1).当点D,E运动多少秒后,△ADE为直角三角形?
(2)在点D,E运动时,线段PD与线段PE相等吗?如果相等,予以证明;如不相等,说明理由.
【答案】(1)![]() ;(2)相等,证明见解析.
;(2)相等,证明见解析.
【解析】
(1)设当点D,E运动![]() 秒后,△ADE为直角三角形,则
秒后,△ADE为直角三角形,则![]() ,
,![]() ,
,![]() ,
,![]() ,根据30°角的直角边=斜边的一半建立方程,求出其解即可;
,根据30°角的直角边=斜边的一半建立方程,求出其解即可;
(2)作DG∥AB交BC于点E,证明△DGP≌△EBP,就可以得出PD=PE.
解:(1)∵△ABC是等边三角形,
∴AB=BC=AC=4cm,∠A=∠ABC=∠C=60°.
设当点D,E运动![]() 秒后,△ADE为直角三角形,
秒后,△ADE为直角三角形,
∴∠ADE=90°,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴∠AED=30°,
∴AE=2AD,
∴![]() ,
,
解得:![]() ;
;
答:当点D,E运动![]() 秒后,△ADE为直角三角形运动;
秒后,△ADE为直角三角形运动;
(2)线段PD与线段PE相等,证明如下:
证明:作DG∥AB交BC于点G,
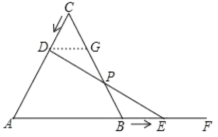
∴∠GDP=∠BEP,∠DGP=∠EBP,∠CDG=∠A=60°,∠CGD=∠ABC=60°,
∴∠C=∠CDG=∠CGD,
∴△CDG是等边三角形,
∴DG=DC,
∵DC=BE,
∴DG=BE.
在△DGP和△EBP中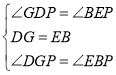 ,
,
∴△DGP≌△EBP(ASA),
∴PD=PE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目