Question

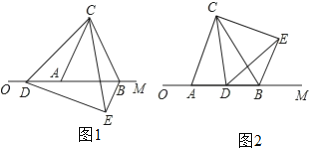
【题目】如图，四边形ABCD是菱形，AB=2，∠ABC=30°，点E是射线DA上一动点，把△CDE沿CE折叠，其中点D的对应点为点D′，若CD′垂直于菱形ABCD的边时，则DE的长为_____．

Answer 1

【答案】或2或2﹣2或2+2．

【解析】

分情况进行讨论：

①当D'C⊥AD时，如图1，根据30度的余弦列式可得DE的长；

②当CD'⊥AB时，如图2，过E作EF⊥CD于F，设CF=EF=x，则ED=2x，DF=x，根据CD=CF+DF=2，列方程可得DE的长；

③当CD'⊥BC时，延长D'C交AD于F，分别计算EF和DF的长，可得DE的长；

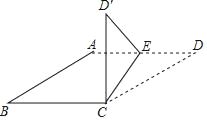
④当D'C⊥CD时，如图4，延长D'C交DE于F，分别计算EF和DF的长，可得DE的长．

分4种情况：

①当D'C⊥AD时，如图1，设DE=D'E=x，

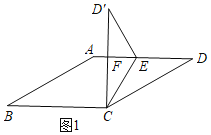
由折叠得：CD=CD'=2，

∵四边形ABCD是菱形，

∴∠D=∠B=30°，

∴∠D=∠D'=30°，

Rt△CFD中，CF=CD=1，

∴D'F=CD'-CF=2-1=1，

Rt△D'FE中，cos30°=，

∴，

∴DE=D'E=；

②当CD'⊥AB时，如图2，过E作EF⊥CD于F，

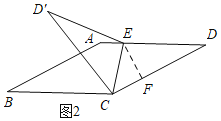
∵AB∥CD，

∴∠B+∠BCD=180°，

∵∠B=30°，

∴∠BCD'=60°，∠DCD'=150°-60°=90°，

由折叠得∠ECD=∠DCD'=45°，

∴△ECF是等腰直角三角形，

设CF=EF=x，则ED=2x，DF=x，

∵CD=CF+DF=2，

∴x+x=2，

x=-1，

∴DE=2x=2-2；

③当CD'⊥BC时，如图3，延长D'C交AD于F，则D'C⊥ED，

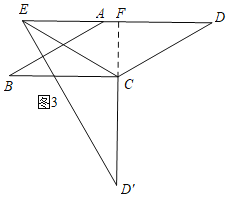
Rt△CFD中，∠D=30°，CD=2，

∴CF=1，DF=，

Rt△D'EF中，D'F=3，∠D'=30°，

∴EF=，

∴DE=EF+DF=2；

④当D'C⊥CD时，如图4，延长D'C交DE于F，

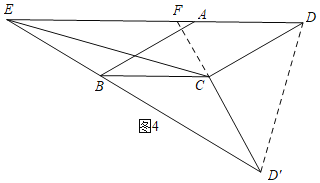
∵∠DCD'=90°，

∴∠FCD=90°，

∵CD=2，∠FDC=30°，

∴CF=，DF=2FC=，

由折叠得：∠ECD=∠ECD'==135°，

∴∠DEC=∠D'EC=15°，

∴∠FEB=∠FD'E=30°，

∴EF=D'F=+2，

∴DE=EF+DF=2+2，

综上所述，DE的长为或2或2-2或2+2．

故答案为或2或2-2或2+2．