题目内容
【题目】如图所示，在Rt△ABC中，∠C=90°，∠A=30°，AB边中点D到BC边距离为3 cm，现在AC边找点E，使BE+ED值最小，则BE+ED的最小值是________cm.
【答案】6
【解析】
将30°的Rt△ABC补成等边三角形
,知点B和点
关于AC对称．连接D交AC于点E，则E即是所求作的点，且BE+ED的最小值即是DE的长．
解：如图：作点B关于AC对称点，DF⊥BC,连接A,D. ，则
的长为BE+ED的最小值
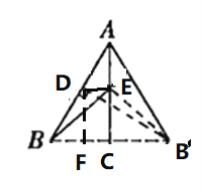
在Rt△ABC中，∠ACB=90°，AB边中点D到BC边距离为3 cm，DF⊥BC
∴DF=3，∠DFB=∠ACB=90°
∴DF//AC
∵D为AB边中点，DF//AC
∴AC=2DF=6
∵点B、点关于AC对称, ∠BAC=30°
∴
, 
∴
∴
是等边三角形
∴
又∵
∴
=6
∴BE+ED的最小值即是DE的长为:6．
故答案为:6
练习册系列答案
相关题目
