Question

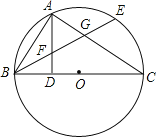
【题目】如图，已知∠ABC，①BD平分∠ABC；②DE=DF；③∠ABC+∠EDF=180°，以①②③中的两个作为条件，另一个作为结论，可以使结论成立的有几个（ ）

A.0个B.1个C.2个D.3个

Answer 1

【答案】D

【解析】

过D作DM⊥AB于M，DN⊥BC于N，分三种情况，分别推出△END≌△FMD即可．

如图：作DM⊥BA于点M，DN⊥BC于点N,

(1)①BD平分∠ABC；②DE=DF；作为条件，③∠ABC+∠EDF=180°作为结论

因为BD平分∠ABC, DM⊥BA，DN⊥BC,

所以DM=DN，∠DNE=∠DMF= 90°

又因为DE=DF，

所以△DEN≌△DFM

所以∠DEN=∠DFM,

因为∠DEB +∠CED =180°,

所以∠DEB +∠BFD= 180°

所以在四边形BEDF中,

∠ABC+∠EDF = 360°-180°= 180°,

即∠ABC+∠EDF = 180° (3) 作为结论成立;

(2) ①BD平分∠ABC；③∠ABC+∠EDF=180°；作为条件，②DE=DF作为结论

因为BD平分∠ABC, DM⊥BA，DN⊥BC,

所以DM=DN，∠DNE=∠DMF= 90°,

因为∠ABC+∠EDF=180°,

所以在四边形BEDF中,∠DEB +∠BFD = 360°- 180°= 180°,

因为∠DEB +∠CED =180°,

所以∠DEN=∠DFM

所以△DEN≌△DFM

所以DE=DF, (2) 作为结论成立;

(3) ②DE=DF；③∠ABC+∠EDF=180°；作为条件，①BD平分∠ABC作为结论

因为∠ABC+∠EDF=180°,

所以在四边形BEDF中,∠DEB +∠BFD = 360°- 180°= 180°,

因为∠DEB +∠CED =180°,

所以∠DEN=∠DFM

因为DM⊥BA，DN⊥BC,

所以∠DNE=∠DM F= 90°,

因为DE=DF

所以△DEN≌△DFM

所以DM=DN

因为DM⊥BA，DN⊥BC, DM=DN

所以BD平分∠ABC(1) 作为结论成立;

故：有3种情况满足题干要求

故选：D