��Ŀ����
����Ŀ��ֱ������ϵ�У���֪A��1��0�����Ե�AΪԲ�Ļ�Բ����M��4��4���ڡ�A�ϣ�ֱ��y=��![]() x+b����M���ֱ�x�ᡢy����B��C���㣮
x+b����M���ֱ�x�ᡢy����B��C���㣮
��1������գ���A�İ뾶Ϊ�� ����b=�� ����������д�����̣�
���ж�ֱ��BC���A��λ�ù�ϵ����˵�����ɣ�
��2����EF�С�A�ڵ�F�ֱ�AB��BC��G��E����FE��BC����![]() ��ֵ��
��ֵ��
��3������P�ڡ�A�ϣ���Q��y����һ�����ڵ�C�·�������PQMΪ����ֱ��������ʱ��ֱ��д����Q�����꣮


���𰸡�(1) 5��7;(2) ����,���ɼ�����;(3) Q�������ǣ�0��0����0��2����0����8����0��3��![]() ����
����
��������
��1��������AM����M��MQ��x����Q�����AQ��QM�����ݹ��ɶ������AM���ɣ���M������������ʽ�����b���ɣ������B��C�����֤꣬��AQM����BQM���ƣ��Ƴ���MAQ=��BMQ���Ƴ���AMB=90�����ɣ�
��2����EG=a�����ݹ��ɶ������BC��AC��CM��ֵ��������BEG����BOC���ƣ����BE��ֵ��������BEG����AFG���ƣ����GF��ֵ������BC=BE+EM+CM���������a���ɣ�
��3��������������ٵ���PQM=90��ʱ��MQ=PQ��������Գƣ��ó�Q��O�غϣ��������Q�����ꣻ�ڵ���PMQ=90�㣬MQ=MP����MD��x��MH��y��֤��MHQ�ա�MDP���Ƴ�P��Բ��x�����ύ�㣬��������𰸣��۵���QPM=90��ʱ���������������һ�����P��y������P��m��n����Q��0��b���ó����̢�4-m=n-b����4-n=-m������1-m��2+n2=52���ⷽ���鼴�����b���ڶ������P��y���ҷ���ͬ�������b��ֵ��
��1���ٽ⣺����AM����M��MQ��x����Q��

��AQ=4��1=3��MQ=4��
�ɹ��ɶ����ã�AM=![]() =5��
=5��
��M��4��4������y=��![]() x+b�ã�4=��
x+b�ã�4=��![]() ��4+b��
��4+b��
��b=7��
�ʴ�Ϊ��5��7��
�ڽ⣺���У�
�����ǣ�����AF��

y=��![]() x+7��
x+7��
��x=0ʱ��y=7����C��0��7����OC=7��
��y=0ʱ��0=��![]() x+7��
x+7��
��x=![]() ��
��
��B��![]() ��0����OB=
��0����OB=![]() ��
��
��BQ=OB��OQ=![]() ��4=
��4=![]() ��AQ=4��1=3��MQ=4��
��AQ=4��1=3��MQ=4��
��![]() =
=![]() =
=![]() ��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
�ߡ�MQA=��MQB��
���AMQ�ס�MBQ��
���MAQ=��BMQ��
�ߡ�MAQ+��AMQ=90�㣬
���AMQ+��BMQ=90�㣬
��AM��BC��
��ֱ��BC���A��λ�ù�ϵ�����У�
��2���⣺����AC��

����COB�У��ɹ��ɶ����ã�BC=![]() =
=![]() ��
��
ͬ��AC=5![]() ��
��
��AM=5���ɹ��ɶ����ã�CM=5��
��EG=a��
��EF��BC��
���FEB=��COB=90�㣬
�ߡ�OBC=��OBC��
���BEG�ס�BOC��
��![]() ��
��
��![]() =
=![]() ��
��
��BE=![]() a��
a��
��������߳������ã�EM=EF=BC��BE��CM=![]() ��
��![]() a��5��
a��5��
��EF��CB��AF��EF��
��AF��BC��
���AFG�ס�BEG��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��FG=![]() ��
��
��BE+EM+CM=BC��
��![]() a+a+
a+a+![]() +5=
+5=![]() ��
��
a=![]() ��
��
EG=![]() ��FG=
��FG=![]() ��
��
��![]() =
=![]() =3��
=3��
��3���⣺�ٵ���PQM=90��ʱ��MQ=PQ���ɶԳ���M��P����X��Գƣ�
����Q��O�غ���Q��0��0����
�ڵ���PMQ=90�㣬MQ=MP����MD��x��MH��y��
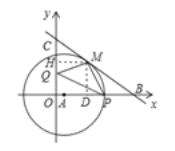
�ɵ���MHQ�ա�MDP��
��P��Բ��x�����ύ��
�Ӷ�Q��0��2����
�۵���QPM=90��ʱ�������������
��һ�����P��y������ͼ��

��P��m��n����Q��0��b���ɵã�
��4��m=n��b����4��n=��m������1��m��2+n2=52��
�ⷽ����ã�b=2��b=��8��b=2Ҳ�����������������bͬ����ֱ�Dz�ͬ����
�ڶ������P��y���ҷ���ͬ���ã�
��m��4=n��b����4��n=m������1��m��2+n2=52��
�ⷽ����ã�b=3+![]() ���ᣩ��b=3��
���ᣩ��b=3��![]() ��
��
�ۺ�������Q�������ǣ�0��0����0��2����0����8����0��3��![]() ����
����