[题目]如图.在△ABC中.E为AC的中点.AD平分∠BAC.BA:CA=2:3.AD与BE相交于点O.若△OAE的面积比△BOD的面积大1.则△ABC的面积是( )A. 8 B. 9 C. 10 D. 11 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在△ABC中，E为AC的中点，AD平分∠BAC，BA：CA=2：3，AD与BE相交于点O，若△OAE的面积比△BOD的面积大1，则△ABC的面积是（　　）

A. 8 B. 9 C. 10 D. 11

【答案】C

【解析】

作DM⊥AC于M，DN⊥AB于N．首先证明BD：DC=2：3，设△ABC的面积为S．则S△ADC=S，S△BEC=S，构建方程即可解决问题；

解：作DM⊥AC于M，DN⊥AB于N．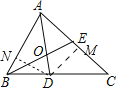

∵AD平分∠BAC，DM⊥AC于M，DN⊥AB于N，
∴DM=DN，

∴S△ABD：S△ADC=BD：DC=ABDN：ACDM=AB：AC=2：3，

设△ABC的面积为S．则S△ADC=S，S△BEC=S，
∵△OAE的面积比△BOD的面积大1，
∴△ADC的面积比△BEC的面积大1，
∴S-S=1，

∴S=10，
故选：C．

练习册系列答案

A. 19.2° B. 8° C. 6° D. 3°

【题目】一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（）
A.5：4
B.5：2
C. ：2
D. ：

【题目】2012义乌市）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1 ．
（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；
（2）如图2，连接AA1 ， CC1 ．若△ABA1的面积为4，求△CBC1的面积；
（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1 ，求线段EP1长度的最大值与最小值．

【题目】如图，在菱形ABCD中，AB=4，取CD中点O，以O为圆心OD为半径作圆交AD于E，交BC的延长线交于点F，
（1）若cos∠AEB= ，则菱形ABCD的面积为；
（2）当BE与⊙O相切时，AE的长为．

【题目】如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面说法中正确的序号是_____．

①△ABE的面积等于△BCE的面积；②∠AFG=∠AGF；③∠FAG=2∠ACF；④BH=CH．

【题目】如图，在平面直角坐标系中有一个轴对称图形，A（3，-2），B（3，﹣6）两点在此图形上且互为对称点，若此图形上有一个点C（﹣2，+1）．

（1）求点C的对称点的坐标．

（2）求△ABC的面积．

【题目】如图，点E正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．

（1）求证：△ABF≌△CBE；
（2）判断△CEF的形状，并说明理由．

【题目】某中学为了解学生的课外阅读情况，就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查（每位同学仅选一项），并根据调查结果制作了尚不完整的频数分布表：

类别	频数（人数）	频率
文学	m	0.42
艺术	22	0.11
科普	66	n
其他	28
合计		1

（1）表中m= ， n=；
（2）在这次抽样调查中，最喜爱阅读哪类读物的学生最少？
（3）根据以上调查，试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人？

试题分类